Pearls from the swines

Retention time prediction is dead, long live retention order index prediction!

by

We just solved a problem that I never wanted to solve: That is, transferable retention time prediction of small molecules. They say that the best king is someone who does not want to be king; so maybe, the best problem solver is someone who does not want to solve the problem? Not sure about that. (My analogies have been quite monarchist lately; we are watching too much The Crown.)

What is transferable retention time prediction? Let’s assume you tell me some details about your chromatographic setup. We are talking about liquid, reversed-phase chromatography. You tell me what column you use, what gradient, what pH, maybe what temperature. Then, you say “3-Ketocholanic acid” and I say, “6.89 min”. You say “Dibutyl phthalate”, I say “7.39 min”. That’s it, folks. If you think that is not possible: Those are real-world examples from a biological dataset. The true (experimentally measured) retention times where 6.65 min and 7.41 min.

Now, you might say, “but how many authentic standards were measured on the same chromatographic setup so that you could do your predictions”? Because that is how retention time prediction works, right? You need authentic standards measured on the same system so that you can do predictions, right? Not for transferable retention time prediction. For our method, the answer to the above question is zero, at least in general. For the above real-world example, the answer is 19. Nineteen. In detail, 19 NAPS (N-Alkylpyridinium 3-sulfonate) molecules were measured in an independent run. Those standards were helpful, but we could have done without them. If you know a bit about retention time prediction: There was no fine-tuning of some machine learning model on the target dataset. No, sir.

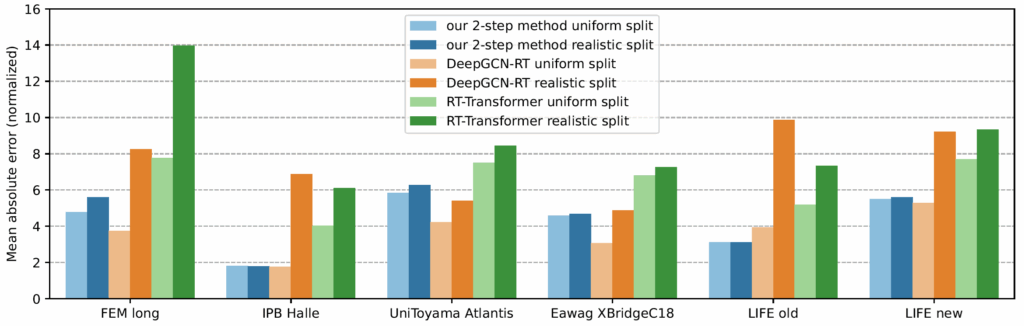
Now comes the cool part: Our method for retention time prediction already performs better than any other method for retention time prediction. The performance is almost as good as that of best-in-class methods if we do a random (uniform) split of the data on the target system. Yet, we all know (or, we all should know) that uniform splitting of small molecules is not a smart idea; it results in massively overestimating the power of machine learning models. Now, our model is not trained (fine-tuned) on data from the target system. Effect: Our method works basically equally well for any splitting of the target dataset. And, we already outperform the best-in-class method.

Evaluation results for (transferable) retention time predictions on six datasets

Why am I telling you that? I mean, besides showing off? (I sincerely hope that you share my somewhat twisted humor.) And, why did I say “already” above? Thing is, retention time prediction is dead, and you might not want to ruin your PhD student’s career by letting him/her try to develop yet another machine learning model for retention time prediction. But now, there is a new, much cooler task for you and/or your PhD student!

  • If you are into graph machine learning, have a look at the problem of retention order index (ROI) prediction. This problem is both challenging and relevant, I can guarantee you that. Different from somewhat ill-posed problems of predicting complex biological traits such as toxicity, there is good reason to believe that ROI prediction can ultimately be “solved”, meaning that predictions become more accurate than experimental errors. On the other hand, ROI prediction is challenging, so complex & intricate models can demonstrate their power. Data are already available for thousands of compounds, trending upward. In conjunction with our 2-step approach, a better model for ROI prediction will automatically result in a better method for transferable retention time prediction. To give a ballpark estimate on the relevance: There are more than 2.1 million scientific studies that use liquid chromatography for the analysis of small molecules, and the chromatography market has an estimated yearly volume of 4 to 5 billion Euro. Your method may allow users to predict retention times for compounds that are illegal to have in the lab (be it tetrodoxin or cocaine), for all compounds in all spectral libraries and molecular structure databases combined, for compounds that do not even exist or which we presently do not know about.
  • If you are doing LC experiments, you might want to upload your LC dataset with authentic standards to RepoRT. I would assume that our 2-step method (see below for details) will be integrated into many computational tools for compound annotation shortly; at least for one method I am sure. Alternatively, you might want to use 2-step to plan you next experiment, maximizing the separation of your compounds. Now, the 2-step method can truly do transferable prediction of retention times: It can do the predictions even for columns that are altogether missing from the training data. But things get easier and predictions get more accurate if there is a dataset in the training data with exactly your chromatographic setup. Let’s not make things overly complicated: A grandmaster in chess may be able to play ten games blindfolded and simultaneously, but s:he would not do so unless it is absolutely necessary. To this end, upload your reference datasets now, get better predictions in the very near future! It does not matter what compounds are in your dataset, as long as it contains a reasonable number (say, 100) of compounds. Everything helps; and in particular, it will help your own predictions for your chromatographic setup!

Now, how does the 2-step method work? The answer is: We do not try to predict retention times, because that is impossible. Instead, we train a machine learning model that predicts a retention order index. A retention order index (ROI) is simply a real-valued number, such as 0.123 or 99999. The model somehow integrates the chromatographic conditions, such as the used column and the mobile phase. Given two compounds A and B from some dataset (experiment) where A elutes before B, we ask the model to predict two number x (for compound A) and y (for compound B) such that x < y holds. If we have an arbitrary chromatographic setup, we use the predicted ROIs of compounds to decide in which order the compounds elute in the experiment. And that is already the end of the machine learning part. But I promised you transferable retention time, and now we are stuck with some lousy ROI? Thing is, we found that you can easily map ROIs to retention times. All you need is a low-degree polynomial, degree two was doing the trick for us. No fancy machine learning needed, good old curve fitting and median regression will do the trick. To establish the mapping, you need a few compounds where you know both the (predicted) ROI and the (measured) retention time. These may be authentic standards, such as the 19 NAPS molecules mentioned above. If you do not have standards, you can also use high-confidence spectral library hits. This can be an in-house library, but a public library such as MassBank will also work. Concentrate on the 30 best hits (cosine above 0.85, and 6+ matching peaks); even if half of these annotations are wrong, you may construct the mapping with almost no error. And voila, you can now predict retention times for all compounds, for exactly this chromatographic setup! Feed the compound into the ROI model, predict a ROI, map the ROI to a retention time, done. Read our preprint to learn all the details.

At this stage, you may want to stop reading, because the rest is gibberish; unimportant “historical” facts. But maybe, it is interesting; in fact, I found it somewhat funny. I mentioned above that I never wanted to work on retention time prediction. I would have loved if somebody else would have solved the problem, because I thought my group should stick with the computational analysis of mass spectrometry data from small molecules. (We are rather successful doing that.) But for a very long time, there was little progress. Yes, models got better using transfer learning (pretrain/fine-tune paradigm), DNNs and transformers; but that was neither particularly surprising nor particularly useful. Not surprising because it is an out-of-the-textbook application of transfer learning; not particularly useful because you still needed training data from the target system to make a single prediction. How should we ever integrate these models with CSI:FingerID?

In 2016, Eric Bach was doing his Master thesis and later, his PhD studies on the subject, under the supervision of Juho Rousu at Aalto University. At some stage, the three of us came up with the idea to consider retention order instead of retention times: Times were varying all over the place, but retention order seemed to be easier to handle. Initially, I thought that combinatorial optimization was the way to go, but I was wrong. Credit to whom credit is due: Juho had the great idea to predict retention oder instead of retention time. For that, Eric used a Ranking Support Vector Machine (RankSVM); this will be important later. This idea resulted in a paper at ECCB 2018 (machine learning and bioinformatics are all about conference publications) on how to predict retention order, and how doing so can (very slightly) improve small molecule annotation using MS/MS. (Eric and Juho wrote two more papers on the subject.)

The fact that Eric was using a RankSVM had an interesting consequence: The RankSVM is trained on pairs of compounds, but what it is actually predicting is a single real-valued number, for a given compound structure. For two compounds, we then compare the two predicted numbers; the smaller number tells you the compound that is eluting first. In fact, the machine learning field of learning-to-rank does basically the same, in order to decide which website best fits with your Google DuckDuckGo query. I must say that back then, I did not like this approach at all; it struck me as overly complicated. But after digesting it for some time, I had an idea: What if we do not use ROIs to decide which compounds elutes first? What if we instead map these ROIs to retention times, using non-linear regression? Unfortunately, I never got Eric interested to go into this direction. And I tried; yes I tried.

About seven years ago, Michael Witting and I rather reluctantly decided to jointly go after the problem. (I would not dare to go after a problem that requires massive chemical intuition without an expert; if you are a chemist, I hope you feel the same about applying machine learning.) We had my crazy idea of mapping ROIs to retention times, and a few backup plans in case this would fail. We had two unsuccessful attempts to secure funding from the Deutsche Forschungsgemeinschaft. My favorite sentence from the second round rejection is, “this project should have been supported in the previous round as the timing would have been better”; we all remember how the field of retention time prediction dramatically changed from 2018 to 2019…? But as they say, it is the timing, stupid! We finally secured funding in May 2019; and I could write, “and the rest is history”. But alas, no. Because the first thing we had to learn was that there was no (more precisely, not enough) training data. Jan Stanstrup had done a wonderful but painstaking job to manually collect datasets “from the literature” for his PredRet method. Yet, a lot of metadata were missing (these data are not required for PredRet, we must not complain) and we had to dig into the literature and data to close those gaps. Also, we clearly needed more data to train a machine learning model. With this, our hunt for more data began, which we partly scraped from publications, partly measured on our own; kudos go to Eva Harrieder! This took much, much longer than we would ever have expected, and resulted in the release of RepoRT in 2023. Well, after that, it is the usual. It works, it doesn’t work, maybe it works; next, it is all bad again; the other methods are so much better; the other methods have memory leakage; now, we have memory leakage; and finally, success. Phew… And here it is.

What about HILIC? I have no idea; but I can tell you that it is substantially more complicated. In fact, there currently is not even a description of columns comparable to HSM and Tanaka for RP. Maybe, somebody wants to get something started? Also, HILIC columns are much more diverse than RP columns, meaning that we need more training data (currently, we have less) and a better way to describe the column than for RP. But hey, start now so that it is ready in 10 years; worked for us!

References

  • Kretschmer, F., Harrieder, E.-M., Witting, M., Böcker, S. Times are changing but order matters: Transferable prediction of small molecule liquid chromatography retention times. ChemRxiv, https://doi.org/10.26434/chemrxiv-2024-wd5j8-v3, 2024. Version 3 from August 2025.
  • Bach, E., Szedmak, S., Brouard, C., Böcker, S. & Rousu, J. Liquid-Chromatography Retention Order Prediction for Metabolite Identification. Bioinformatics 34. Proc. of European Conference on Computational Biology (ECCB 2018), i875–i883 (2018). [DOI]
  • Bach, E., Rogers, S., Williamson, J. & Rousu, J. Probabilistic framework for integration of mass spectrum and retention time information in small molecule identification. Bioinformatics 37, 1724–1731 (2021). [DOI]
  • Bach, E., Schymanski, E. L. & Rousu, J. Joint structural annotation of small molecules using liquid chromatography retention order and tandem mass spectrometry data. Nat Mach Intel 4, 1224–1237 (2022). [DOI]
  • Stanstrup, J., Neumann, S. & Vrhovšek, U. PredRet: prediction of retention time by direct mapping between multiple chromatographic systems. Anal Chem 87, 9421–9428 (2015). [DOI]
  • Snyder, L. R., Dolan, J. W. & Carr, P. W. The hydrophobic-subtraction model of reversed-phase column selectivity. J Chromatogr A 1060, 77–116 (2004). [DOI]
  • Kimata, K., Iwaguchi, K., Onishi, S., Jinno, K., Eksteen, R., Hosoya, K., Araki, M. & Tanaka, N. Chromatographic Characterization of Silica C18 Packing Materials. Correlation between a Preparation Method and Retention Behavior of Stationary Phase. J Chromatogr Sci 27, 721–728 (1989). [DOI]

How many small molecules could be out there?

by

Every (put a large number here) days I stumble over the question, “how large is the universe of small molecules?” in a publication or a blog. Not the number of small molecules that we already “know” – those are covered in databases such as HMDB, PubChem or ZINC. (Although many compounds in PubChem etc. are purely hypothetical, too.) Not the number of metabolites that actually exist in nature. Also, we do not care if these small molecules are synthesizable with current technology. Rather, we want to know: How large is the space of small molecules that could exist? These could be natural small molecules (natural products, secondary metabolites) or synthetic compounds. I usually do not like the numbers that people report as “the truth”, as one estimate was taken out of context and started to develop a life of its own. Hence, I thought I write down what I know.

Obviously, we have to first define precisely what we actually counting. Since the problem is already hard enough, we usually do not care about 3d considerations (usually including stereochemistry), and simply ask for the number of molecular graphs (chemical 2d structures). On the one hand, resulting estimates are a lower bound, as adding stereochemistry into the mix results in more structures; on the other hand, resulting estimates are upper bounds, in the sense that many molecular graphs that we draw, cannot exist in 3d space. For the sake of simplicity, let’s forget about this problem.

Next, we have to define what a “small molecule” actually is. Usually, we simply apply a threshold on the mass of the molecule, such as “all molecules below 1000 Dalton“. If you prefer, you may instead think of “molecular weight”; this is the expected mass of the molecule, taken over all isotopologues and, hence, slightly larger. Yet, people usually consider mass in these considerations. Maybe, because mass spectrometry is one of the (maybe, the) most important experimental technology for the analysis of small molecules; maybe, because isotopes make a big difference for small molecules. Since our bounds on mass are somewhat arbitrary, anyways, this is not a big problem: Why exactly 1000 Dalton? Is prymnesin-B1 a small molecules? It is not a peptide, not a lipid, not a macromolecule, and it sure looks like a biological small molecule; it is just “too heavy” (1819.5 Dalton). For our calculations we will stick with the mass of 1000 Dalton; yet, it all still applies when you want to use a different threshold, and doing so is actually very simple, see below.

Now, the number of small molecules that people are reporting and repeating, making this number “more and more true” (to the point that Google Gemini will return that number as the correct answer when you query with Google) comes from a paper by Bohacek et al. (1997). The caption of Figure 6 contains the sentence “A subset of molecules containing up to 30 C, N, O, and S atoms may have more than 1060 members”. The authors make some back-of-the-envelope calculations in a long footnote, to further support this claim. The authors clearly state that the actual numbers they are giving are incorrect, for each step of their calculations. These calculations are merely meant to demonstrate that the true number is enormously huge; and, that the actual number is not that important, and might never be known to mankind. Unfortunately, many readers did not grasp the second part of what the authors were saying and instead, starting reporting the number “1060 small molecules” as if this number had been calculated for good. From there, it was only a small step into a Science/Nature news (I have to search for it), publications, websites, and finally, the “knowledge” of a large language model such as Gemini. The Wikipedia article about Chemical Space is much more cautious, and also mentions the 500 Dalton cutoff that Bohacek et al. assumed, as they were interested in pharmacologically active molecules. Funnily, Google Gemini does not link to the Wikipedia article, but rather to a “random” website that cites the number of Bohacek et al..

Let us see if we can do better than that. First, we look at a few things that are known. The On-Line Encyclopedia of Integer Sequences (OEIS) gives us loads of helpful numbers:

  • Alkanes are hydrocarbons (carbohydrates with no oxygen) with the “minimal” molecular formula Cn H2n+2 and have no multiple bonds, a tree structure, and no cycles. The number of alkanes can be found in sequence A000628, see also here. Yet, this sequence counts each individual stereoisomer, different from what we said above. The sequence A000602 counts different stereoisomers as identical. For upper bound 1000 Dalton we use n = 71 (nominal mass 996 Dalton), and this is 1 281 151 315 764 638 215 613 845 510 structures, about 1.28 · 1027, or 1.28 octillion. Clearly, not all of them are possible; yet, the number of of “impossible” structures may be smaller than one may think. Alkanes are small molecules, so this is a lower bound on the number of small molecules of this mass.
  • In fact, we can approximate – in the colloquial and in the mathematical sense – this number using the closed formula (i.e. the formula has no recurrences)
    0.6563186958 · n-5/2 · 2.815460033n,
    see Table 3 and equation (16) here (reprint here). For n = 71 this approximation is 1.279 · 1027, which is already pretty close to the true (exact) number. Importantly, this allows us to classify the growth as exponential, meaning that increasing n by one, we have to multiply the number of molecules by a constant (roughly 2.8). We can safely ignore the non-exponential part of the equation, as its influence will get smaller and smaller when n increases. Exponential growth might appear frightening, and in most application domains it would be our enemy; but for counting small molecules, it is actually our friend, as we will see next.
  • Molecules are no trees, they have cycles. So, another idea to get an idea on the number of small molecules is to count simple, connected graphs. “Simple” means that we do not allow multiple edges between two nodes (vertices). We have different types of bounds (single, double, etc.) but multi-edges means that there can be 1000 edges between two nodes, and that is definitely not what we want. We also ignore that we have different elements, that is, labeled nodes. This number is found in sequence A001349. This number growths super-exponential, meaning that it growths faster (for n to infinity) than any exponential function. That is fast, and we indeed observe that already for reasonable number of nodes, numbers become huge: For n = 19 nodes it is 645 465 483 198 722 799 426 731 128 794 502 283 004 (6.45 · 1038) simple graphs; for n = 49 we already have 1.69 · 10291 simple graphs. That is a lot, compare to the number of alkanes. Even more intimidating is the growth: Going from n = 49 to n = 50 nodes we reach 1.89 x 10304 simple graphs, a factor of 11 258 999 068 424 (11 trillion) for a single node added. Suddenly, factor 2.8 does not look that bad any more, does it?
  • Now, one can easily argue that simple graphs are too general: The number of edges incident to (touching) a node is not restricted, whereas it is clearly restricted for molecular graphs. For simplicity, let us consider Carbon-only molecules; carbon has valence 4. Let us further simplify things by only considering cases where each node is connected to exactly 4 other nodes (chemically speaking, no hydrogen atoms, no double bonds). The number of 4-regular, simple, connected graphs is sequence A006820. Given that there is a single such graph for n = 6, it might be surprising how quickly numbers are increasing even for moderate number of nodes n: For n = 28 there are 567 437 240 683 788 292 989 (5.67 · 1020) such graphs.

All of these numbers give us a first impression of the number of small molecules we could consider. Yet, none of them give us any precise number to work with: The number of alkanes is just a lower bound, the number of simple graphs is too large, and the number of 4-regular simple graphs is simultaneously too large (we cannot simply demand that two Carbon atoms are connected, we somehow have to realize that in 3d) and too small (4-regular, Carbon-only). That is not very satisfactory. Yet, we can already learn a few important things:

  • The coefficient c before the 10k is actually not very important. If we are dealing with numbers as large as 10100, then a mere factor of below ten does not make a substantial difference. It is the exponent that is relevant. Similarly, it does not make a relevant change if we think about mass or nominal mass.
  • If we have exponential growth, as we did for alkanes, then it is straightforward to calculate your own estimate in case you are unhappy with the upper bound on mass of 1000 Dalton. Say, you prefer 500 Dalton; then, the estimate for the number of alkanes goes from 1027 to 1027/2 = 3.16 · 1013. Similarly, for 1500 Dalton, we reach 1027·1.5 = 3.16 · 1040 alkanes.

Yet, we can also look at the problem empirically: There exist different methods (the commercial MOLGEN, OMG, MAYGEN, and currently the fastest-tool-in-town, Surge) to generate molecular structures for a given molecular formula. For example, Ruddigkeit et al. generated “all” small molecule structures with up to 17 heavy atoms (CNOS and halogens). I put the “all” in apostrophes because the authors used highly aggressive filters (ad hoc rules on, does a molecule make sense chemically? etc.) to keep the numbers small. With that, they generated the GDB-17 database containing 166 443 860 262 (1.66 · 1011) molecular structures. Unfortunately, only about 0.06% of that databases are publicly available. Also, the aggressive filtering is diametral to our question, how many molecular structures exit.

More interesting for us is a paper from 2005: That year, Kerber et al. published the paper “Molecules in silico: potential versus known organic compounds“. For the paper, the authors generated all small molecule structures with nominal mass up to 150 Dalton, over the set of elements CHNO, using MOLGEN. For example, MOLGEN constructs 615 977 591 molecular structures for mass 150 Dalton. This paper also contains the highly informative Figure 1, where the authors plot the number of (theoretical) molecular structure against nominal mass m. Looking at the plot, I could not resist to see exponential growth, which (if you use a logarithmic y-axis) comes out as a simple line. Remember that exponential growth is our friend.

number of molecular graph with regression line

So, let’s do that formally: I fitted a regression line to the empirical numbers (see Chapter 10 here), and what comes out of it is that we can approximate the number of small molecules between 80 and 150 Dalton as 2.0668257909 · 10−4 · 1.2106212044m. Be warned that there is not the slightest guarantee that growth will continue like that for masses larger than 150 Dalton; it is highly unlikely that growth might slow down, but given that the number of simple graphs is growing superexponentially, maybe the same is true here? I cannot tell you, I am not that much into counting and enumerating graphs. But in any case, my Milchmädchenrechnung should make a much better estimate than anything we have done so far; to be precise, much better than anything else I have ever heard of. For nominal mass 1000 Dalton this number is 2.11 · 1079 molecular structures.

But wait! The above formula tells us the (very approximate) number of all small molecules with mass exactly 1000 Dalton; what we want to know is the number of molecules with mass up to 1000 Dalton. Fun fact about exponential growth: These numbers are basically the same, with a small factor. Recall that the number of molecules with mass m equals a · xm. Pretty much every math student has to prove, during his first year, the equation
\sum_{i=0}^m x^m = \frac{x^{m+1}-1}{x-1}.
To this end, if we want to know the number of molecules with mass up to 1000 Dalton, we simply use the number of molecules with mass exactly 1000 Dalton, and apply a small correction. In detail, the number of molecules with mass up to 1000 Dalton is (almost exactly) 1.21062 / (1.21062 – 1) = 5.74786 times the number of molecules with mass exactly 1000 Dalton. We reach an estimate of 1.21 · 1080 small molecules over elements CHNO with mass up to 1000 Dalton. For mass up to 500 Dalton it is about 1040 molecules (which tells us that the inital estimate was rather far off, and I do not expect that even a superexponential growth could correct that); for mass up to 1500 Dalton it is 10120 small molecules.

But, alas, this estimate is for elements CHNO only; what if we add more elements to the mix? For halogens it is mainly fluorine that will substantially increase the number of molecular structures: Halogens are much heavier than hydrogen. If we replace a single H by F in a molecular structure, then the nominal mass of the molecule increases by 8. The above estimate tells us that there are only 1/4.61 = 0.216 times the molecular structures to consider if we decrease the mass by 8. On the “plus side” we can replace any H by F to reach a different molecule, if we gallantly ignore the problem of isomorphic graph structures. For more than one fluorine, the combinatorics of where we can add them growths polynomially; but at the same time, the number of structures we start from decreases exponentially. Hence, one should not expect a substantially higher number if we add fluorine to the mix; and an even smaller effect for the other halogens. More worrying, from a combinatorial standpoint, are the elements sulfur and phosporus. In particular sulfur with valence 6 could wreak havoc of our estimates. I don’t know what happens if you allow an arbitrary number of S and P; I also don’t know if we would even want such all-sulfur molecules. The only number that I can report is again from the Kerber et al. paper: They also generated all molecular structures for nominal mass 150 Dalton and elements CHNOSiPSFClBrI, using the (unrealistic) fixed valences 3 for phosphorus and 2 for sulfur, resulting in 1 052 647 246 structures, compared to 615 977 591 molecular structures over elements CHNO. Yet, this small increase in structures (merely doubled, phew) should not lull us into a false sense of security: Not only the unrealistic valences, even more so the relatively small mass could mean that in truth, the number of structures with sulfur and phosphorus is substantially higher. I suggest we stick with the number 1080 and in the back of our minds, keep the note “it is likely even worse”.

It is not easy to grasp a number as large as 1080, so a few words to get a feeling:

  • The number 1080 is 100 septemvigintillion, or 100 million billion billion billion billion billion billion billion billions. If we have a name for it, it cannot be that bad.
  • The observable universe contains an estimated 1080 atoms. If we had the technology to build a computer that uses every single atom of the observable universe as its memory, and where we need only a single atom to store the complete structure of a small molecule, then the observable universe would be “just right” to store all small molecules up to 1000 Dalton.
  • Using the same technology, molecules up to 1010 Dalton would be absolutely impossible to store, and 1100 Dalton would be absurd. For molecules up to 2000 Dalton you would need 1080 observable universes. Alternatively, a technology that puts a complete universe into a single atom, and does so for each and every atom of this universe. See the final scene of Men in Black.
  • For comparison, the total amount of storage on planet Earth is, at the moment, something like 200 zettabytes, mostly on magnetic tapes. If we could store every molecular structure in 2 bytes, this would allow us to store 1023 molecular structures. If we could now again fold all the storage into a single byte, and again, and again, we reach – after four iterations of folding – the required memory.
  • If we have a computer enumerating molecular structures at a rate of 1 billion structures per second, then we could enumerate 3.15 · 1016 structures per year, and it would take 3.17 · 1063 years to enumerate them all. For comparison, the estimated age of the universe is 1.38 · 1010 years. We would need more than 1050 universes to finish our calculations, where in each universe we have to start our computations with the big bang.
  • Maybe, it helps if we use all computers that exist on planet Earth? Not really; there are maybe 10 billion computers (including smartphones) on Earth, but let’s make it 1000 billion, to be on the safe side. The required time to enumerate all structures drops to 3.17 · 1051 years.
  • But maybe, we can use a quantum computer? Grover’s algorithm brings down the running times to O(\sqrt{n}) if we have to consider n objects. Again assuming that our quantum computer could do 1 billion such computations per second, we would end up with a running time of 1031 seconds, or 3.17 · 1023 years. That is still a looong time. There might be smarter ways of processing all structures on a quantum computer than using Grover’s algorithm; but so far, few such algorithms for even fewer problems have been found.

Now, 1080 is a large number, and you might thing, “this is the reason why dealing with small molecules is so complicated!” But that is a misconception. It is trivial to find much larger numbers that a computer scientist has to deal with every day; just a few examples from bioinformatics: The number of protein sequences of length 100 is 1.26 · 10130.  Yet, we can easily work with longer protein sequences. The number of pairwise alignments for two sequences of length 1000 is 2.07 · 10600. Yet, every bioinformatics student learns during his/her first year how to find the optimal alignment between two sequences, sequences that may be much longer than 1000 bases. The thing is, sequences/strings are simple structures, and we have learned to look only for the interesting, i.e. optimal alignments. (Discrete optimization is great!) What makes dealing with small molecule structures complicated is that these structures are themselves rather complicated (graphs, when even trees can be a horror, ask someone from phylogenetics) plus at the same time, there are so many, which prevents us from simply enumerating them all, then doing the complicated stuff for every structure.

That’s all, folks! Hope it helps.

Yet another blog

by

Hi all, I thought I put my blog post (singular) into its own category. Not sure about the title, that may change. Why another blog when there is already this great blog on metabolomics and mass spectrometry? Because here I may talk about computational stuff as well, such as failed evaluations of machine learning methods (that one never gets old). I hope to write something once every four fortnights, let’s see how that works out. :shrug:

False Discovery Rates for metabolite annotation: Why accurate estimation is impossible, and why this should not stop us from trying

by

I recently gave a talk at the conference of the Metabolomics society. After the talk, Oliver Fiehn asked, “when will we finally have FDR estimation in metabolite annotation?” This is a good question: False Discovery Rates (FDR) and FDR estimation have been tremendously helpful in genomics, transcriptomics and proteomics. In particular, FDRs have been extremely helpful for peptide annotation in shotgun proteomics. Hence, when will FDR estimation finally become a reality for metabolite annotation from tandem mass spectrometry (MS/MS) data? After all, the experimental setup of shotgun proteomics and untargeted metabolomics using Liquid Chromatography (LC) for separation, are highly similar. By the way, if I talk about metabolites below, this is meant to also include other small molecules of biological interest. From the computational method standpoint, they are indistinguishable.

My answer to this question was one word: “Never.” I was about to give a detailed explanation for this one-word answer, but before I could say a second word, the session chair said, “it is always good to close the session on a high note, so let us stop here!” and ended the session. (Well played, Tim Ebbels.) But this is not how I wanted to answer this question! In fact, I have been thinking about this question for several years now; as noted above, I believe that it is an excellent question. Hence, it might be time share my thoughts on the topic. Happy to hear yours! I will start off with the basics; if you are familiar with the concepts, you can jump to the last five paragraphs of this text.

The question that we want to answer is as follows: We are given a bag of metabolite annotations from an LC-MS/MS run. For every query spectrum, this is the best fit (best-scoring candidate) from the searched database, and will be called “hit” in the following. Can we estimate the fraction of hits that are incorrect? Can we do so for a subset of hits? More precisely, we will sort annotations by some score, such as the cosine similarity for spectral library search. If we only accept those hits with score above (or below, it does not matter) a certain threshold, can we estimate the ratio of incorrect hits for this particular subset? In practice, the user selects an arbitrary FDR threshold (say, one percent), and we then find the smallest score threshold so that the hits with score above the score threshold have an estimated FDR below or equal to the FDR threshold. (Yes, there are two thresholds, but we can handle that.)

Let us start with the basic definition. For a given set of annotations, the False Discovery Rate (FDR) is the number of incorrect annotations, divided by the total number of annotations. FDR is usually recorded as a percentage. To compute FDR, you have to have complete knowledge; you can only compute it if you know upfront which annotations are correct and which are incorrect. Sad but true. This value is often referred to as “exact FDR” or “true FDR”, to distinguish it from the estimates we want to determine below. Obviously, you can compute exact FDR for metabolite annotations, too; the downside is that you need complete knowledge. Hence, this insight is basically useless, unless your are some demigod or all-knowing demon. For us puny humans, we do not know upfront which annotations are correct and which are incorrect. The whole concept of FDR and FDR estimation would be useless if we knew: If we knew, we could simply discard the incorrect hits and continue to work with the correct ones.

To this end, a method for FDR estimation tries to estimate the FDR of a given set of annotations, without having complete knowledge. It is important to understand the part that says, “tries to estimate”. Just because a method claims it is estimating FDR, does not mean it is doing a good job, or even anything useful. For example, consider a random number generator that outputs random values between 0 and 1: This IS an FDR estimation method. It is neither accurate nor useful, but that is not required in the definition. Also, a method for FDR estimation may always output the same, fixed number (say, always-0 or always-1). Again, this is a method for FDR estimation; again, it is neither accurate nor useful. Hence, be careful with papers that claim to introduce an FDR estimation method, but fail to demonstrate that these estimates are accurate or at least useful.

But how can we demonstrate that a method for FDR estimation is accurate or useful? Doing so is somewhat involved because FDR estimates are statistical measures, and in theory, we can only ask if they are accurate for the expected value of the estimate. Yet, if someone presents a novel methods for FDR estimation, the minimum to ask for is a series of q-value plots that compare estimated q-values and exact q-values: A q-value is the smallest FDR for which a particular hit is part of the output. Also, you might want to see the distribution of p-values, which should be uniform. You probably know p-values; if you can estimate FDR, chances are high that you can also estimate p-values. Both evaluations should be done for multiple datasets, to deal with the stochastic nature of FDR estimation. Also, since you have to compute exact FDRs, the evaluation must be done for reference datasets where the true answer is known. Do not confuse “the true answer is known” and “the true answer is known to the method“; obviously, we do not tell our method for FDR estimation what the true answer is. If a paper introduces “a method for FDR estimation” but fails to present convincing evaluations that the estimated FDRs are accurate or at least useful, then you should be extremely careful.

Now, how does FDR estimation work in practice? In the following, I will concentrate on shotgun proteomics and peptide annotation, because this task is most similar to metabolomics. There, target-decoy methods have been tremendously successful: You transform the original database you search in (called target database in the following) into a second database that contains only candidates that are incorrect. This is the decoy database The trick is to make the candidates from the decoy database “indistinguishable” from those in the target database, as further described below. In shotgun proteomics, it is surprisingly easy to generate a useful decoy database: For every peptide in the target database, you generate a peptide in the decoy database for which you read the amino acid sequence from back to front. (In more detail, you leave the last amino acid of the peptide untouched, for reasons that are beyond what I want to discuss here.)

To serve its purpose, a decoy database must fulfill three conditions: (i) There must be no overlap between target and decoy database; (ii) all candidates from the decoy database must never be the correct answer; and (iii), false hits in the target database have the same probability to show up as (always false) hits from the decoy database. For (i) and (ii), we can be relatively relaxed: We can interpret “no overlap” as “no substantial overlap”. This will introduce a tiny error in our FDR estimation, which is presumably irrelevant in comparison to the error that is an inevitable part of FDR estimation. For (ii), this means that whenever a search with a query spectrum returns a candidate from the target database, this is definitely not the correct answer. The most important condition is (iii), and if we look more precisely, we will even notice that we have to demand more: That is, the score distribution of false hits from the target database is identical to the score distribution of hits from the decoy database. If our decoy database fulfills all three conditions, then we can use a method such as Target-Decoy Competition and utilize hits from the decoy database to estimate the ration of incorrect hits from the target database. Very elegant in its simplicity.

Enough of the details, let us talk about untargeted metabolomics! Can we generate a decoy database that fulfills the three requirements? Well — it is difficult, and you might think that this is why I argue that FDR estimation is impossible here: Looks like we need a method to produce metabolite structure that look like true metabolites (or, more generally, small molecules of biological interest — it does not matter). Wow, that is already hard — we cannot simply use random molecular structure, because they will not look like the real thing, see (iii). In fact, a lot of research is currently thrown at this problem, as it would potentially allow us to find the next super-drug. Also, how could we guarantee not to accidentally generate a true metabolite, see (ii)? Next, looks like we need a method to simulate a mass spectrum for a given (arbitrary) molecular structure. Oopsie daisies, that is also pretty hard! Again, ongoing research, far from being solved, loads of papers, even a NeurIPS competition coming up.

So, are these the problems we have to solve to do FDR estimation, and since we cannot do those, we also cannot do FDR? In other words, if — in a decade or so — we would finally have a method that can produce decoy molecular structures, and another method that simulates high-quality mass spectra, would we have FDR estimation? Unfortunately, the answer is, No. In fact, we do not even need those methods: In 2017, my lab developed a computational method that transforms a target spectral library into a decoy spectral library, completely avoiding the nasty pitfalls of generating decoy structures and simulating mass spectra. Also, other computational methods (say, naive Bayes) completely avoid generating a decoy database.

The true problem is that we are trying to solve a non-statistical problem with a statistical measure, and that is not going to work, no matter how much we think about the problem. I repeat the most important sentence from above: “False hits in the target database have the same probability to show up as hits from the decoy database.” This sentence, and all stochastic procedure for FDR estimation, assume that a false hit in the target database is something  random. In shotgun proteomics, this is a reasonable assumption: The inverted peptides we used as decoys basically look random, and so do all false hits. The space of possible peptides is massive, and the target peptides lie almost perfectly separated in this ocean of non-occurring peptides. Biological peptides are sparse and well-separated, so to say. But this is not the case for metabolomics and other molecules of biological interest. If an organism has learned how to make a particular compound, it will often also be able to synthesize numerous compounds that are structurally extremely similar. A single hydrogen replaced by a hydroxy group, or vice versa. A hydroxy group “moving by a single carbon atom”. Everybody who has ever looked at small molecules, will have noticed that. Organisms invest a lot of energy to make proteins for exactly this purpose. But this is not only a single organism; the same happens in biological communities, such as the microbiota in our intestines or on our skin. It even happens when no organisms are around. In short: No metabolite is an island.

Sadly, this is the end of the story. Let us assume that we have identified small molecule A for a query MS/MS when in truth, the answer should be B. In untargeted metabolomics and related fields, this usually means that A and B are structurally highly similar, maybe to the point of a “moving hydroxy group”. Both A and B are valid metabolites. There is nothing random or stochastic about this incorrect annotation. Maybe, the correct answer B was not even in the database we searched in; potentially, because it is a “novel metabolite” currently not known to mankind. Alternatively, both compounds were in the database, and our scoring function for deciding on the best candidate simply did not return the correct answer. This will happen, inevitably: Otherwise, you again need a demigod or demon to build the scoring function. Consequently, speaking about the probability of an incorrect hit in the target database, cannot catch the non-random part of such incorrect hits. There is no way to come up with an FDR estimation method that is accurate, because the process itself is not stochastic. Maybe, some statisticians will develop a better solution some day, but I argue that there is no way to ever “solve it for good”, given our incomplete knowledge of what novel metabolites remain to be found out there.

Similar arguments, by the way, hold true for the field of shotgun metaproteomics: There, our database contains peptides from multiple organisms. Due to homologous peptide sequences in different organisms, incorrect hits are often not random. In particular, there is a good chance that if PEPTIDE is in your database, then so is PEPITDE. Worse, one can be in the database you search and one in your biological sample. I refrain from discussing further details; after all, we are talking about metabolites here.

But “hey!”, you might say, “Sebastian, you have published methods for FDR estimation yourself!” Well, that is true: Beyond the 2017 paper mentioned above, the confidence score of COSMIC is basically trying to estimate the Posterior Error Probability of a hit, which is a statistical measure again closely related to FDRs and FDR estimation. Well, you thought you got me there, did you? Yet, do you remember that above, I talked about FDR estimation methods that are accurate or useful? The thing is: FDR estimation methods from shotgun proteomics are enviably accurate, with precise estimates at FDR 1% and below. Yet, even if our FDR estimation methods in metabolomics can never be as accurate as those from shotgun proteomics, that does not mean they cannot be useful! We simply have to accept the fact that our numbers will not be as accurate, and that we have to interpret those numbers with a grain of salt.

The thing is, ballpark estimates can be helpful, too. Assume you have to jump, in complete darkness, into a natural pool of water below. I once did that, in a cave in New Zealand. It was called “cave rafting”, not sure if they still offer that type of organized madness. (Just checked, it does, highly recommended.) Back then, in almost complete darkness, our guide told me to jump; that I would fall for about a meter, and that the water below was two meters deep. I found this information to be extremely reassuring and helpful, but I doubt it was very accurate. I did not do exact measurements after the jump, but it is possible that I fell for only 85cm; possibly, the water was 3m deep. Yet, what I really, really wanted to know at that moment, was: Is it an 8m jump into a 30cm pond? I would say the guide did a good job. His estimates were useful.

I stress that my arguments should not be taken as an excuse to do a lazy evaluation. Au contraire! As a field, we must insist that all methods marketed as FDR estimation methods, are evaluated extensively as such. FDR estimations should be as precise as possible, and evaluations as described above are mandatory. Because only this can tell us how for we can trust the estimates. Because only this can convince us that estimates are indeed useful. Trying to come up with more accurate FDR estimates is a very, very challenging task, and trying to do so may be in vain. But remember: We choose to do these things, not because they are easy, but because they are hard.

I got the impression that few people in untargeted metabolomics and related fields are familiar with the concept of FDR and FDR estimation for annotation. This strikes me as strange, given the success of these concepts in other OMICS fields. If you want to learn more, I do not have the perfect link or video for you, but I tried my best to explain it in my videos about COSMIC, see here. If you have a better introduction, let me know!

Funny side note: If you were using a metascore, your FDR estimates from target-decoy competition would always be 0%. As noted, a method for FDR estimation must not return accurate or useful values, and a broken scoring can easily also break FDR estimation. Party on!

Visualizing the universe of small biomolecules

by

Have you ever wanted to look at the universe of biomolecules (small molecules of biological interest, including metabolites and toxins)? Have you ever wondered how your own dataset fits into this universe? In our preprint, we introduce a method to do just that, using MCES distances to create a UMAP visualization. Onto this visualization, any compound-dataset can be projected, see the interactive example below. In case it is slow, download the code here. Move your mouse over any dot to see the underlying molecular structure.

If you are wondering, “where did the lipids go?”, check this out. See the preprint on why we excluded them above. Looking at commonly used datasets for small molecule machine learning, big differences can be seen in the coverage of the biomolecule space. For example, the toxicity datasets Tox21 and ToxCast appear to rather uniformly cover the universe of biomolecules. In contrast, SMRT is a massive retention time dataset, but appears to be concentrated on a specific area of the compound space. The thing is: One must not expect a machine learning model trained on only a small part of the “universe of biomolecules”, to be applicable to the whole universe. This is a little too much to be asked. Hence, visualizing your data in this way may give you a better understanding of what your machine learning model is actually doing, where it will thrive and where it might fail.

To compare molecular structures, we compute the MCES (Maximum Common Edge Subgraph) of the two molecular structures. Doing so is not new, but comes at the prize that computing a single distance is already an NP-hard problem, see below. Then, why on Earth are we not using Tanimoto coefficients computed from molecular fingerprints, just like everybody else does? Tanimoto coefficients and related fingerprint-based similarity and dissimilarity measures have a massive advantage over all other means of comparing molecular structures: As soon as you have computed the fingerprints of all molecular structures, computing Tanimoto coefficients is blindingly fast. Hence, if you are querying a database, molecular fingerprints are likely the method of choice. We ourselves have been and are heavily relying on molecular fingerprints: CSI:FingerID is predicting molecular fingerprints from MS/MS data, CANOPUS is predicting compound classes from molecular fingerprints, and COSMIC is using Tanimoto coefficients because they are, well, fast. Yet, if you have ever worked with molecular fingerprints and, in particular, Tanimoto coefficients yourself, you must have also noticed their peculiarities, quirks and shortcomings. In fact, from the moment people used Tanimoto coefficients, others have warned about these unexpected and highly undesirable behaviors; an early example is by Flower (1998). On the one hand, a Tanimoto coefficient of below 0.7 can be the result of two compounds with only one hydroxy group added. On the other hand, two highly different compounds, one half the size of the other, may also have a Tanimoto coefficient of 0.7. Look at the two examples below: According to the Tanimoto coefficient, the two structures on the left are less similar than the two on the right. Does that sound right? By the way: The same holds true for any fingerprint-based similarity or dissimilarity measure, and also for any other fingerprint type. These are examples but the problem is universal.

In contrast, the MCES distance is much more intuitive to interpret, as it is the edit distance between molecule graphs and, hence, nicely represents our intuition of chemical reactions. For example, adding an hydroxy group results in an MCES distance of one. Don’t get us wrong: The MCES distance is not perfect, either. First and foremost, the MCES problem is NP-hard; hence, computing a single exact distance between two molecules might take days or weeks. We can happily report that we have “solved” this issue by introducing the myopic MCES distance: We first quickly compute a lower bound on the true distance. If this bound tells us that the true distance is larger than 22, then we would argue that knowing the exact value (maybe 22, maybe 25, maybe 32) is of little help: These two molecules are very, very different, full stop. But if we find that the lower bound only guarantees that the distance is small (say, at most 20) then we use exact computations based on solving an Integer Linear Program. With some more algorithm engineering, we were able to bring down computation time to fractions of a second. And that means that we were able to compute all distances for a set of 20k biomolecular structures, plus several well-known machine learning datasets, in reasonable time and on our limited compute resources. (Sadly, we still do not own a supercomputer.) You will not be able to do all-against-all with a million molecular structures, so if your research requires to do so, you might have to stick with the Tanimoto coefficient, quirky as it is. Yet, we found that subsampling does indeed give us rather reproducible results, see Fig. 7 of the preprint (page 23).

There are other shortcomings of the MCES distance: For example, it is not well-suited to capture the fact that one molecular structure is a substructure of the other. This is unquestioned, but what is also true, is: The MCES distance does not have peculiarities or quirks. The fact that it does not capture substructures, can be readily derived from its definition; this behavior is by design. In case you do not like the absolute MCES distance, because you think that large molecules are treated unfairly, then feel free to normalize it using the size of the molecules. Now that we can (relatively) swiftly compute the myopic MCES distance, we can play around with it.

We used UMAP (Uniform manifold approximation and projection) to visualize the universe of biomolecules but, honestly, we don’t care. You prefer t-SNE? Use that! You prefer a tree-based visualization? Use that! See the following comparison (from left to right UMAP, t-SNE and a Minimum Spanning Tree), created in just a few minutes. Or, maybe Topological Data Analysis? Fine, too! All those visualizations have their pros and cons, and one should always keep Pachter’s elephant in the back of one’s brain. But the thing is: We know that the space of molecular structures has an intrinsic structure, and we are merely using the different visualization methods to get a feeling for its intrinsic structure.

UMAP
t-SNE
Minimum Spanning Tree

Now, one peculiarity of the above UMAP plots must be mentioned here: When comparing different ML training datasets, we re-used the UMAP embedding computed from the biomolecular structures alone (Fig. 3 in the preprint). Yet, UMAP will neatly integrate any new structures into the existing “compound universe” even if those new structures are very, very different from the ones that were used to compute the projection. This is by design of UMAP, it interpolates, all good. So, we were left with two options: Recompute the embedding for every subplot? This would allow us to spot if a dataset contains compounds very different from all biomolecular structures, but would result in a “big mess” and an uneven presentation. Or, should we keep the embedding fixed? This makes a nicer plot but hides “alien compounds”. We went with the second option solely because the overall plot “looks nicer”; in practice, we strongly suggest to also compute a new UMAP embedding.

In the preprint, we discuss two more ways to check whether a training dataset provides uniform coverage of the biological compound space: We examine the compound class distribution, to check whether certain compound classes are “missing” in our training dataset. And finally, we use the Natural Product-likeness score distribution to check for lopsidedness. All of that can give you ideas about the data you are working with. There have been numerous scandals about machine learning models repeating prejudice in the training data; don’t let the distribution of molecules in your training data let you draw conclusions which, at closer inspection, might be lopsided or even wrong.

If you want to compute myopic MCES distances yourself, find the source code here. You will need a cluster node, or proper patience if you do computations on your laptop. All precomputed myopic MCES distances from the preprint can be found here. We may also be able to help you with further computations.

MAD HATTER correctly annotates 98% of small molecule MS/MS searching in PubChem

by

We are thrilled to announce that our newest tool MAD HATTER can correctly annotate 98% of small molecule tandem mass spectra, when searching in PubChem! We are extremely excited about this massive breakthrough! MAD HATTER combines CSI:FingerID results with information from the searched structure database via a metascore, using viable compound information such as the melting point, or the number of “was it a cat I saw?” in the compound description.

Our evaluations use the well-known CASMI 2016 data, and we are happy to announce that MAD HATTER strongly outperforms all tools that participated in the contest. MAD HATTER also performs very well if we replace the MS/MS spectra by either empty spectra or random spectra. This opens up fantastic new venues in the future, where instrument vendors may replace bulky and expensive traps and collision cells by a random number generators or /dev/null.

Read the exciting preprint on bioRxiv: https://doi.org/10.1101/2022.12.07.519436

We assume that everybody will be thrilled to use MAD HATTER in the future. At the moment, you may find additional information here, here and here.

Update: Read the exciting final paper in Metabolites: https://doi.org/10.3390/metabo13030314

Why we do not use metascores

by

…and why you should also be very careful when doing so

Hi all, I (Sebastian) have recorded a talk about metascores which is now available from our YouTube channel at https://www.youtube.com/watch?v=mkfG6-ZqD0s. With “metascores”, I mean scores that are not based on the actual data (or metadata!) but rather on side information such as citation counts or production volumes of metabolites. See below for the distinction between metascores and metadata.

I have been thinking about recording such a talk for several years now. I never did, partly because I hoped that this topic would “go away” without me doing such a video. I was wrong, metascores are still in much use today. The other reason not recording the talk was that the more I thought about metascores, the more problems came into my mind. So, I added more slides to the talk, and then I had to re-record the talk, and so on ad infinitum. I now present six problems in the video; I decided I better record it before a seventh problem pops up.

I want to make clear that there is nothing bad with metascores as long as you are using them for a confined application: That is, you want to identify one particular feature in your LC-MS run, and for that you need some candidate compounds to get things started. If this is what you are after, and the actual identification is performed by an independent method (say, buying a commercial standard and doing a spike-in experiment) then you can generate the sorted list of candidates by any method that suits you; that clearly includes metascores. But as soon as you are doing “untargeted metabolomics” or anything similar to that, and as soon as you are using annotations of an in silico method to derive downstream information, you are in trouble — as explained in the video.

I discuss six problems of metascores in the talk, and I thought I will also shortly discuss them here. But first, let us discuss metascores vs. metadata.

Metascores vs. metadata

I previously had some discussions about metascores, and I have come to believe that some people think highly of metascores because of the connection to metadata. Well, point is, this is merely a misunderstanding. Metascores and metadata have nothing in common but the prefix “meta”. Metadata is data about your data; it is already used by in silico methods, be it the mass accuracy of the measurement or the ion mode. Metascores — at least the ones I am aware of — use side information, information which has nothing to do with the actual experiment you are conducting. See here for details. Side note: Using such side information (priors) has been discussed repeatedly in other fields such as transcriptomics or proteomics, but has been abandoned everywhere else many years ago.

1st problem: Blockbuster metabolites

This is potentially the biggest single issue of metascores: You will annotate the same metabolites again and again. They are simply “so much cooler” than everything else that a method can basically ignore the data. Who will not love to watch another blockbuster movie? And who will not love to annotate another blockbuster metabolite? See here for details.

2nd problem: Evaluation results are misleading

This is not so much a problem of metascores, but one that is caused by the interplay of metascores and the data we use for evaluations. In short, do not trust evaluations of metascores; the data used for evaluating them are basically from blockbuster metabolites. Which metascores will then correctly annotate, because they love to annotate blockbuster metabolites, and only blockbuster metabolites. See here for details.

3rd problem: Obfuscating good search results

When I say that metascore methods can basically ignore the MS/MS data, this is not as good as it may sound. These methods will obfuscate high-quality search results of an in silico method, and make it impossible for you to decide whether or not a particular search result is worth to follow up on. This issue gets dramatic if you use annotations to generate, say, statistics about the sample. In short: Never do any further analysis on annotations when a metascore was in play. See here for details.

4th problem: Why are you using MS/MS anyways?

It turns out that using a metascore, you can actually forget about MS/MS data; in evaluations, this data are no longer needed to reach good annotation rates. Isn’t that great news: We can do untargeted metabolomics and get away with LC-MS data, saving ourselves the troubles of recording MS/MS data at all! A classical win-win situation: Faster measurements and untargeted metabolomics. Citing Leonard Hofstadter: “Our babies will be smart and beautiful.” See here for details.

5th problem: You are not searching where you think you are

This problem makes me nervous, personally. We are basically saying we are searching throughout the whole planet Earth when in fact, we are searching only in our apartment. I doubt that I can get across the implications of doing so; but this is a horror for reproducibility, method disclosure etc. See here for details.

6th problem: Overfitting

But citations are a reasonable feature for compound annotation, right? And, metascores using citation numbers improve search results, right? Doesn’t that mean something? Short answer: No. We can also reach excellent search results with a metascore that is using moonstruck features such as “number of consonants in the PubChem synonyms”. See here for details.

I also have a few suggestions how I would proceed, instead of using a metascore. I am convinced that these suggestions are not the final word; rather, they are meant as a starting point.

Hope this talk helps to clear the perception of this particular computational method. Best regards, Sebastian.