After three weeks, our web server (and many other things) are back online. We made sure that CSI:FingerID etc are up and running, but somehow forgot that there is more than that. Sorry in case this caused any troubles.
Sebastian Böcker
Retention time prediction is dead, long live retention order index prediction!
We just solved a problem that I never wanted to solve: That is, transferable retention time prediction of small molecules. They say that the best king is someone who does not want to be king; so maybe, the best problem solver is someone who does not want to solve the problem? Not sure about that. (My analogies have been quite monarchist lately; we are watching too much The Crown.)
What is transferable retention time prediction? Let’s assume you tell me some details about your chromatographic setup. We are talking about liquid, reversed-phase chromatography. You tell me what column you use, what gradient, what pH, maybe what temperature. Then, you say “3-Ketocholanic acid” and I say, “6.89 min”. You say “Dibutyl phthalate”, I say “7.39 min”. That’s it, folks. If you think that is not possible: Those are real-world examples from a biological dataset. The true (experimentally measured) retention times where 6.65 min and 7.41 min.
Now, you might say, “but how many authentic standards were measured on the same chromatographic setup so that you could do your predictions”? Because that is how retention time prediction works, right? You need authentic standards measured on the same system so that you can do predictions, right? Not for transferable retention time prediction. For our method, the answer to the above question is zero, at least in general. For the above real-world example, the answer is 19. Nineteen. In detail, 19 NAPS (N-Alkylpyridinium 3-sulfonate) molecules were measured in an independent run. Those standards were helpful, but we could have done without them. If you know a bit about retention time prediction: There was no fine-tuning of some machine learning model on the target dataset. No, sir.
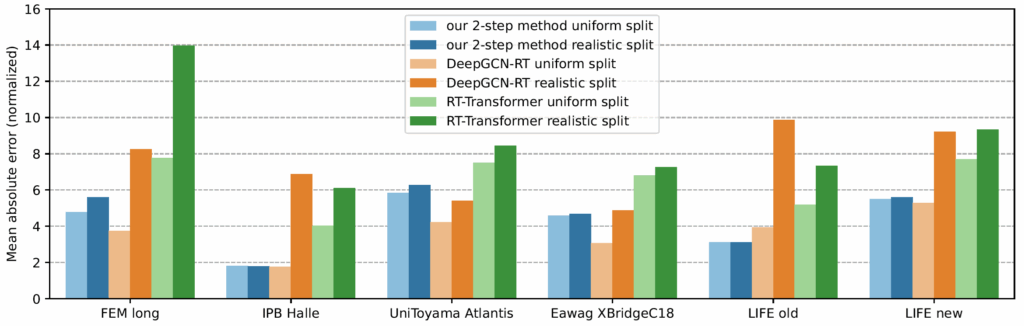
Now comes the cool part: Our method for retention time prediction already performs better than any other method for retention time prediction. The performance is almost as good as that of best-in-class methods if we do a random (uniform) split of the data on the target system. Yet, we all know (or, we all should know) that uniform splitting of small molecules is not a smart idea; it results in massively overestimating the power of machine learning models. Now, our model is not trained (fine-tuned) on data from the target system. Effect: Our method works basically equally well for any splitting of the target dataset. And, we already outperform the best-in-class method.
Why am I telling you that? I mean, besides showing off? (I sincerely hope that you share my somewhat twisted humor.) And, why did I say “already” above? Thing is, retention time prediction is dead, and you might not want to ruin your PhD student’s career by letting him/her try to develop yet another machine learning model for retention time prediction. But now, there is a new, much cooler task for you and/or your PhD student!
- If you are into graph machine learning, have a look at the problem of retention order index (ROI) prediction. This problem is both challenging and relevant, I can guarantee you that. Different from somewhat ill-posed problems of predicting complex biological traits such as toxicity, there is good reason to believe that ROI prediction can ultimately be “solved”, meaning that predictions become more accurate than experimental errors. On the other hand, ROI prediction is challenging, so complex & intricate models can demonstrate their power. Data are already available for thousands of compounds, trending upward. In conjunction with our 2-step approach, a better model for ROI prediction will automatically result in a better method for transferable retention time prediction. To give a ballpark estimate on the relevance: There are more than 2.1 million scientific studies that use liquid chromatography for the analysis of small molecules, and the chromatography market has an estimated yearly volume of 4 to 5 billion Euro. Your method may allow users to predict retention times for compounds that are illegal to have in the lab (be it tetrodoxin or cocaine), for all compounds in all spectral libraries and molecular structure databases combined, for compounds that do not even exist or which we presently do not know about.
- If you are doing LC experiments, you might want to upload your LC dataset with authentic standards to RepoRT. I would assume that our 2-step method (see below for details) will be integrated into many computational tools for compound annotation shortly; at least for one method I am sure. Alternatively, you might want to use 2-step to plan you next experiment, maximizing the separation of your compounds. Now, the 2-step method can truly do transferable prediction of retention times: It can do the predictions even for columns that are altogether missing from the training data. But things get easier and predictions get more accurate if there is a dataset in the training data with exactly your chromatographic setup. Let’s not make things overly complicated: A grandmaster in chess may be able to play ten games blindfolded and simultaneously, but s:he would not do so unless it is absolutely necessary. To this end, upload your reference datasets now, get better predictions in the very near future! It does not matter what compounds are in your dataset, as long as it contains a reasonable number (say, 100) of compounds. Everything helps; and in particular, it will help your own predictions for your chromatographic setup!
Now, how does the 2-step method work? The answer is: We do not try to predict retention times, because that is impossible. Instead, we train a machine learning model that predicts a retention order index. A retention order index (ROI) is simply a real-valued number, such as 0.123 or 99999. The model somehow integrates the chromatographic conditions, such as the used column and the mobile phase. Given two compounds A and B from some dataset (experiment) where A elutes before B, we ask the model to predict two number x (for compound A) and y (for compound B) such that x < y holds. If we have an arbitrary chromatographic setup, we use the predicted ROIs of compounds to decide in which order the compounds elute in the experiment. And that is already the end of the machine learning part. But I promised you transferable retention time, and now we are stuck with some lousy ROI? Thing is, we found that you can easily map ROIs to retention times. All you need is a low-degree polynomial, degree two was doing the trick for us. No fancy machine learning needed, good old curve fitting and median regression will do the trick. To establish the mapping, you need a few compounds where you know both the (predicted) ROI and the (measured) retention time. These may be authentic standards, such as the 19 NAPS molecules mentioned above. If you do not have standards, you can also use high-confidence spectral library hits. This can be an in-house library, but a public library such as MassBank will also work. Concentrate on the 30 best hits (cosine above 0.85, and 6+ matching peaks); even if half of these annotations are wrong, you may construct the mapping with almost no error. And voila, you can now predict retention times for all compounds, for exactly this chromatographic setup! Feed the compound into the ROI model, predict a ROI, map the ROI to a retention time, done. Read our preprint to learn all the details.
At this stage, you may want to stop reading, because the rest is gibberish; unimportant “historical” facts. But maybe, it is interesting; in fact, I found it somewhat funny. I mentioned above that I never wanted to work on retention time prediction. I would have loved if somebody else would have solved the problem, because I thought my group should stick with the computational analysis of mass spectrometry data from small molecules. (We are rather successful doing that.) But for a very long time, there was little progress. Yes, models got better using transfer learning (pretrain/fine-tune paradigm), DNNs and transformers; but that was neither particularly surprising nor particularly useful. Not surprising because it is an out-of-the-textbook application of transfer learning; not particularly useful because you still needed training data from the target system to make a single prediction. How should we ever integrate these models with CSI:FingerID?
In 2016, Eric Bach was doing his Master thesis and later, his PhD studies on the subject, under the supervision of Juho Rousu at Aalto University. At some stage, the three of us came up with the idea to consider retention order instead of retention times: Times were varying all over the place, but retention order seemed to be easier to handle. Initially, I thought that combinatorial optimization was the way to go, but I was wrong. Credit to whom credit is due: Juho had the great idea to predict retention oder instead of retention time. For that, Eric used a Ranking Support Vector Machine (RankSVM); this will be important later. This idea resulted in a paper at ECCB 2018 (machine learning and bioinformatics are all about conference publications) on how to predict retention order, and how doing so can (very slightly) improve small molecule annotation using MS/MS. (Eric and Juho wrote two more papers on the subject.)
The fact that Eric was using a RankSVM had an interesting consequence: The RankSVM is trained on pairs of compounds, but what it is actually predicting is a single real-valued number, for a given compound structure. For two compounds, we then compare the two predicted numbers; the smaller number tells you the compound that is eluting first. In fact, the machine learning field of learning-to-rank does basically the same, in order to decide which website best fits with your Google DuckDuckGo query. I must say that back then, I did not like this approach at all; it struck me as overly complicated. But after digesting it for some time, I had an idea: What if we do not use ROIs to decide which compounds elutes first? What if we instead map these ROIs to retention times, using non-linear regression? Unfortunately, I never got Eric interested to go into this direction. And I tried; yes I tried.
About seven years ago, Michael Witting and I rather reluctantly decided to jointly go after the problem. (I would not dare to go after a problem that requires massive chemical intuition without an expert; if you are a chemist, I hope you feel the same about applying machine learning.) We had my crazy idea of mapping ROIs to retention times, and a few backup plans in case this would fail. We had two unsuccessful attempts to secure funding from the Deutsche Forschungsgemeinschaft. My favorite sentence from the second round rejection is, “this project should have been supported in the previous round as the timing would have been better”; we all remember how the field of retention time prediction dramatically changed from 2018 to 2019…? But as they say, it is the timing, stupid! We finally secured funding in May 2019; and I could write, “and the rest is history”. But alas, no. Because the first thing we had to learn was that there was no (more precisely, not enough) training data. Jan Stanstrup had done a wonderful but painstaking job to manually collect datasets “from the literature” for his PredRet method. Yet, a lot of metadata were missing (these data are not required for PredRet, we must not complain) and we had to dig into the literature and data to close those gaps. Also, we clearly needed more data to train a machine learning model. With this, our hunt for more data began, which we partly scraped from publications, partly measured on our own; kudos go to Eva Harrieder! This took much, much longer than we would ever have expected, and resulted in the release of RepoRT in 2023. Well, after that, it is the usual. It works, it doesn’t work, maybe it works; next, it is all bad again; the other methods are so much better; the other methods have memory leakage; now, we have memory leakage; and finally, success. Phew… And here it is.
What about HILIC? I have no idea; but I can tell you that it is substantially more complicated. In fact, there currently is not even a description of columns comparable to HSM and Tanaka for RP. Maybe, somebody wants to get something started? Also, HILIC columns are much more diverse than RP columns, meaning that we need more training data (currently, we have less) and a better way to describe the column than for RP. But hey, start now so that it is ready in 10 years; worked for us!
References
- Kretschmer, F., Harrieder, E.-M., Witting, M., Böcker, S. Times are changing but order matters: Transferable prediction of small molecule liquid chromatography retention times. ChemRxiv, https://doi.org/10.26434/chemrxiv-2024-wd5j8-v3, 2024. Version 3 from August 2025.
- Bach, E., Szedmak, S., Brouard, C., Böcker, S. & Rousu, J. Liquid-Chromatography Retention Order Prediction for Metabolite Identification. Bioinformatics 34. Proc. of European Conference on Computational Biology (ECCB 2018), i875–i883 (2018). [DOI]
- Bach, E., Rogers, S., Williamson, J. & Rousu, J. Probabilistic framework for integration of mass spectrum and retention time information in small molecule identification. Bioinformatics 37, 1724–1731 (2021). [DOI]
- Bach, E., Schymanski, E. L. & Rousu, J. Joint structural annotation of small molecules using liquid chromatography retention order and tandem mass spectrometry data. Nat Mach Intel 4, 1224–1237 (2022). [DOI]
- Stanstrup, J., Neumann, S. & Vrhovšek, U. PredRet: prediction of retention time by direct mapping between multiple chromatographic systems. Anal Chem 87, 9421–9428 (2015). [DOI]
- Snyder, L. R., Dolan, J. W. & Carr, P. W. The hydrophobic-subtraction model of reversed-phase column selectivity. J Chromatogr A 1060, 77–116 (2004). [DOI]
- Kimata, K., Iwaguchi, K., Onishi, S., Jinno, K., Eksteen, R., Hosoya, K., Araki, M. & Tanaka, N. Chromatographic Characterization of Silica C18 Packing Materials. Correlation between a Preparation Method and Retention Behavior of Stationary Phase. J Chromatogr Sci 27, 721–728 (1989). [DOI]
One billion queries served
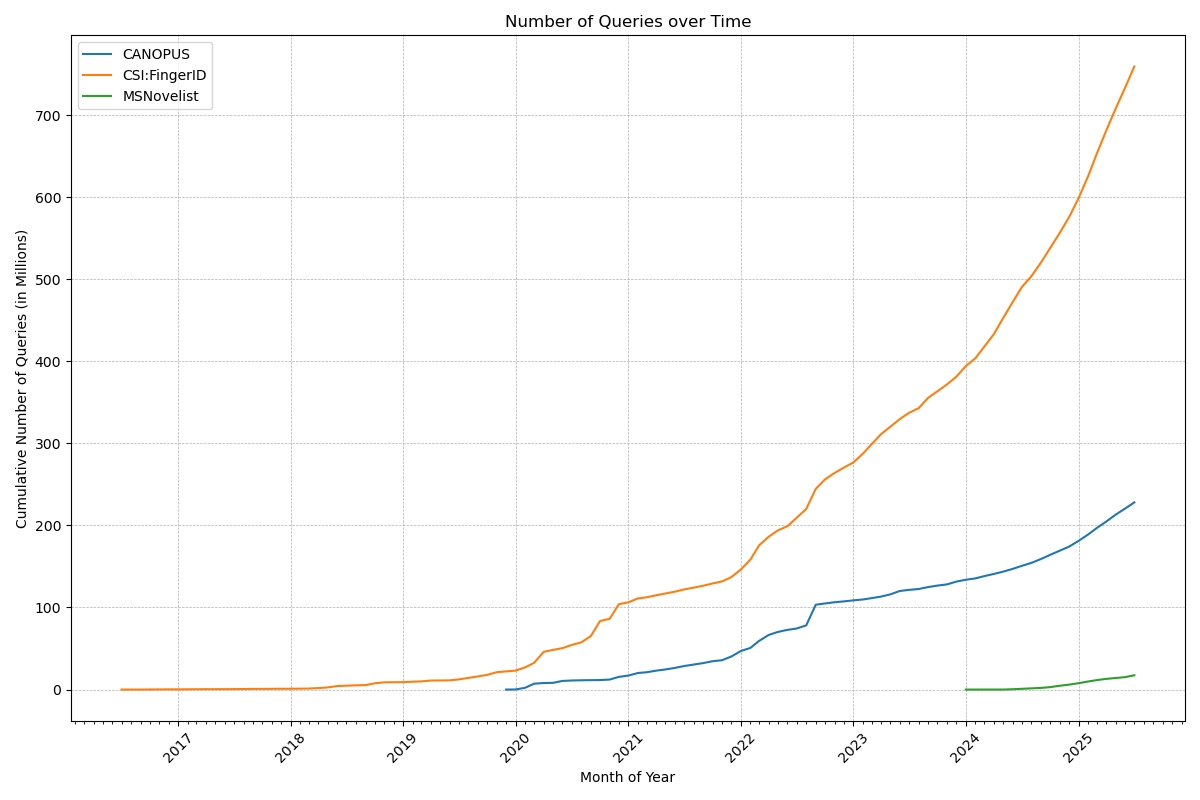
Now, that number deserves a celebration: Our web services have served a billion queries! In detail, the CSI:FingerID web service processed 759 million queries, the CANOPUS web service 228 million, and MSNovelist has 17 million queries. During the last 12 months, 3816 users have processed their data using our web services. Excellent!
Remember when Gangnam Style was the first video on YouTube to hit 1 billion views? That was a big thing in December 2012; we do not expect the same amount of media coverage for our first billion, though. 😉 Indeed, one billion is a big number, and it is really hard to grasp it: See this beautiful video by Tom Scott to “understand” the difference between a million and a billion.
Anyways, many thanks to the team (mainly Markus Fleischauer) who make this possible, and who ensure that everything is running so smoothly! It should not be a surprise that processing 1.18 million queries per day (on average!), is a highly non-trivial undertaking. Auto-scalable, self-healing compute infrastructure and highly optimized database infrastructure are key ingredients for keeping small molecule annotations flowing smoothly to our global community.
PS. The one billion also cover the queries processed by the Bright Giant and their servers, who are offering these services to companies. One counter to rule them all…
Sebastian will receive an ERC advanced grant
Excellent news: Sebastian will receive an ERC Advanced Grant from the European Research Council!
In the project BindingShadows, we will develop machine learning models that predict whether some query molecule has a particular bioactivity (say, toxicity) or is binding to a certain protein, where the only information we have about the query molecule is its tandem mass spectrum. The clue is: The model is supposed to do that when the identity and structure of the molecule is not known; not known to us, not known to the person that measured the data, not known to mankind (aka novel compounds).
Clearly, we will not do that for one bioactivity or one protein, but for all of them in parallel. Evolution has, through variation and selection, optimized the structure of small molecules for tasks such as communication and warfare, and the pool of natural products is enriched with bioactive compounds. Our project will try to harvest this information.
Sounds interesting? Looking for a job? Stay tuned, as we will shortly start searching for PhD and postdoc candidates!
How many small molecules could be out there?
Every (put a large number here) days I stumble over the question, “how large is the universe of small molecules?” in a publication or a blog. Not the number of small molecules that we already “know” – those are covered in databases such as HMDB, PubChem or ZINC. (Although many compounds in PubChem etc. are purely hypothetical, too.) Not the number of metabolites that actually exist in nature. Also, we do not care if these small molecules are synthesizable with current technology. Rather, we want to know: How large is the space of small molecules that could exist? These could be natural small molecules (natural products, secondary metabolites) or synthetic compounds. I usually do not like the numbers that people report as “the truth”, as one estimate was taken out of context and started to develop a life of its own. Hence, I thought I write down what I know.
Obviously, we have to first define precisely what we actually counting. Since the problem is already hard enough, we usually do not care about 3d considerations (usually including stereochemistry), and simply ask for the number of molecular graphs (chemical 2d structures). On the one hand, resulting estimates are a lower bound, as adding stereochemistry into the mix results in more structures; on the other hand, resulting estimates are upper bounds, in the sense that many molecular graphs that we draw, cannot exist in 3d space. For the sake of simplicity, let’s forget about this problem.
Next, we have to define what a “small molecule” actually is. Usually, we simply apply a threshold on the mass of the molecule, such as “all molecules below 1000 Dalton“. If you prefer, you may instead think of “molecular weight”; this is the expected mass of the molecule, taken over all isotopologues and, hence, slightly larger. Yet, people usually consider mass in these considerations. Maybe, because mass spectrometry is one of the (maybe, the) most important experimental technology for the analysis of small molecules; maybe, because isotopes make a big difference for small molecules. Since our bounds on mass are somewhat arbitrary, anyways, this is not a big problem: Why exactly 1000 Dalton? Is prymnesin-B1 a small molecules? It is not a peptide, not a lipid, not a macromolecule, and it sure looks like a biological small molecule; it is just “too heavy” (1819.5 Dalton). For our calculations we will stick with the mass of 1000 Dalton; yet, it all still applies when you want to use a different threshold, and doing so is actually very simple, see below.
Now, the number of small molecules that people are reporting and repeating, making this number “more and more true” (to the point that Google Gemini will return that number as the correct answer when you query with Google) comes from a paper by Bohacek et al. (1997). The caption of Figure 6 contains the sentence “A subset of molecules containing up to 30 C, N, O, and S atoms may have more than 1060 members”. The authors make some back-of-the-envelope calculations in a long footnote, to further support this claim. The authors clearly state that the actual numbers they are giving are incorrect, for each step of their calculations. These calculations are merely meant to demonstrate that the true number is enormously huge; and, that the actual number is not that important, and might never be known to mankind. Unfortunately, many readers did not grasp the second part of what the authors were saying and instead, starting reporting the number “1060 small molecules” as if this number had been calculated for good. From there, it was only a small step into a Science/Nature news (I have to search for it), publications, websites, and finally, the “knowledge” of a large language model such as Gemini. The Wikipedia article about Chemical Space is much more cautious, and also mentions the 500 Dalton cutoff that Bohacek et al. assumed, as they were interested in pharmacologically active molecules. Funnily, Google Gemini does not link to the Wikipedia article, but rather to a “random” website that cites the number of Bohacek et al..
Let us see if we can do better than that. First, we look at a few things that are known. The On-Line Encyclopedia of Integer Sequences (OEIS) gives us loads of helpful numbers:
- Alkanes are hydrocarbons (carbohydrates with no oxygen) with the “minimal” molecular formula Cn H2n+2 and have no multiple bonds, a tree structure, and no cycles. The number of alkanes can be found in sequence A000628, see also here. Yet, this sequence counts each individual stereoisomer, different from what we said above. The sequence A000602 counts different stereoisomers as identical. For upper bound 1000 Dalton we use n = 71 (nominal mass 996 Dalton), and this is 1 281 151 315 764 638 215 613 845 510 structures, about 1.28 · 1027, or 1.28 octillion. Clearly, not all of them are possible; yet, the number of of “impossible” structures may be smaller than one may think. Alkanes are small molecules, so this is a lower bound on the number of small molecules of this mass.
- In fact, we can approximate – in the colloquial and in the mathematical sense – this number using the closed formula (i.e. the formula has no recurrences)
0.6563186958 · n-5/2 · 2.815460033n,
see Table 3 and equation (16) here (reprint here). For n = 71 this approximation is 1.279 · 1027, which is already pretty close to the true (exact) number. Importantly, this allows us to classify the growth as exponential, meaning that increasing n by one, we have to multiply the number of molecules by a constant (roughly 2.8). We can safely ignore the non-exponential part of the equation, as its influence will get smaller and smaller when n increases. Exponential growth might appear frightening, and in most application domains it would be our enemy; but for counting small molecules, it is actually our friend, as we will see next. - Molecules are no trees, they have cycles. So, another idea to get an idea on the number of small molecules is to count simple, connected graphs. “Simple” means that we do not allow multiple edges between two nodes (vertices). We have different types of bounds (single, double, etc.) but multi-edges means that there can be 1000 edges between two nodes, and that is definitely not what we want. We also ignore that we have different elements, that is, labeled nodes. This number is found in sequence A001349. This number growths super-exponential, meaning that it growths faster (for n to infinity) than any exponential function. That is fast, and we indeed observe that already for reasonable number of nodes, numbers become huge: For n = 19 nodes it is 645 465 483 198 722 799 426 731 128 794 502 283 004 (6.45 · 1038) simple graphs; for n = 49 we already have 1.69 · 10291 simple graphs. That is a lot, compare to the number of alkanes. Even more intimidating is the growth: Going from n = 49 to n = 50 nodes we reach 1.89 x 10304 simple graphs, a factor of 11 258 999 068 424 (11 trillion) for a single node added. Suddenly, factor 2.8 does not look that bad any more, does it?
- Now, one can easily argue that simple graphs are too general: The number of edges incident to (touching) a node is not restricted, whereas it is clearly restricted for molecular graphs. For simplicity, let us consider Carbon-only molecules; carbon has valence 4. Let us further simplify things by only considering cases where each node is connected to exactly 4 other nodes (chemically speaking, no hydrogen atoms, no double bonds). The number of 4-regular, simple, connected graphs is sequence A006820. Given that there is a single such graph for n = 6, it might be surprising how quickly numbers are increasing even for moderate number of nodes n: For n = 28 there are 567 437 240 683 788 292 989 (5.67 · 1020) such graphs.
All of these numbers give us a first impression of the number of small molecules we could consider. Yet, none of them give us any precise number to work with: The number of alkanes is just a lower bound, the number of simple graphs is too large, and the number of 4-regular simple graphs is simultaneously too large (we cannot simply demand that two Carbon atoms are connected, we somehow have to realize that in 3d) and too small (4-regular, Carbon-only). That is not very satisfactory. Yet, we can already learn a few important things:
- The coefficient c before the 10k is actually not very important. If we are dealing with numbers as large as 10100, then a mere factor of below ten does not make a substantial difference. It is the exponent that is relevant. Similarly, it does not make a relevant change if we think about mass or nominal mass.
- If we have exponential growth, as we did for alkanes, then it is straightforward to calculate your own estimate in case you are unhappy with the upper bound on mass of 1000 Dalton. Say, you prefer 500 Dalton; then, the estimate for the number of alkanes goes from 1027 to 1027/2 = 3.16 · 1013. Similarly, for 1500 Dalton, we reach 1027·1.5 = 3.16 · 1040 alkanes.
Yet, we can also look at the problem empirically: There exist different methods (the commercial MOLGEN, OMG, MAYGEN, and currently the fastest-tool-in-town, Surge) to generate molecular structures for a given molecular formula. For example, Ruddigkeit et al. generated “all” small molecule structures with up to 17 heavy atoms (CNOS and halogens). I put the “all” in apostrophes because the authors used highly aggressive filters (ad hoc rules on, does a molecule make sense chemically? etc.) to keep the numbers small. With that, they generated the GDB-17 database containing 166 443 860 262 (1.66 · 1011) molecular structures. Unfortunately, only about 0.06% of that databases are publicly available. Also, the aggressive filtering is diametral to our question, how many molecular structures exit.
More interesting for us is a paper from 2005: That year, Kerber et al. published the paper “Molecules in silico: potential versus known organic compounds“. For the paper, the authors generated all small molecule structures with nominal mass up to 150 Dalton, over the set of elements CHNO, using MOLGEN. For example, MOLGEN constructs 615 977 591 molecular structures for mass 150 Dalton. This paper also contains the highly informative Figure 1, where the authors plot the number of (theoretical) molecular structure against nominal mass m. Looking at the plot, I could not resist to see exponential growth, which (if you use a logarithmic y-axis) comes out as a simple line. Remember that exponential growth is our friend.
So, let’s do that formally: I fitted a regression line to the empirical numbers (see Chapter 10 here), and what comes out of it is that we can approximate the number of small molecules between 80 and 150 Dalton as 2.0668257909 · 10−4 · 1.2106212044m. Be warned that there is not the slightest guarantee that growth will continue like that for masses larger than 150 Dalton; it is highly unlikely that growth might slow down, but given that the number of simple graphs is growing superexponentially, maybe the same is true here? I cannot tell you, I am not that much into counting and enumerating graphs. But in any case, my Milchmädchenrechnung should make a much better estimate than anything we have done so far; to be precise, much better than anything else I have ever heard of. For nominal mass 1000 Dalton this number is 2.11 · 1079 molecular structures.
But wait! The above formula tells us the (very approximate) number of all small molecules with mass exactly 1000 Dalton; what we want to know is the number of molecules with mass up to 1000 Dalton. Fun fact about exponential growth: These numbers are basically the same, with a small factor. Recall that the number of molecules with mass m equals a · xm. Pretty much every math student has to prove, during his first year, the equation
To this end, if we want to know the number of molecules with mass up to 1000 Dalton, we simply use the number of molecules with mass exactly 1000 Dalton, and apply a small correction. In detail, the number of molecules with mass up to 1000 Dalton is (almost exactly) 1.21062 / (1.21062 – 1) = 5.74786 times the number of molecules with mass exactly 1000 Dalton. We reach an estimate of 1.21 · 1080 small molecules over elements CHNO with mass up to 1000 Dalton. For mass up to 500 Dalton it is about 1040 molecules (which tells us that the inital estimate was rather far off, and I do not expect that even a superexponential growth could correct that); for mass up to 1500 Dalton it is 10120 small molecules.
But, alas, this estimate is for elements CHNO only; what if we add more elements to the mix? For halogens it is mainly fluorine that will substantially increase the number of molecular structures: Halogens are much heavier than hydrogen. If we replace a single H by F in a molecular structure, then the nominal mass of the molecule increases by 8. The above estimate tells us that there are only 1/4.61 = 0.216 times the molecular structures to consider if we decrease the mass by 8. On the “plus side” we can replace any H by F to reach a different molecule, if we gallantly ignore the problem of isomorphic graph structures. For more than one fluorine, the combinatorics of where we can add them growths polynomially; but at the same time, the number of structures we start from decreases exponentially. Hence, one should not expect a substantially higher number if we add fluorine to the mix; and an even smaller effect for the other halogens. More worrying, from a combinatorial standpoint, are the elements sulfur and phosporus. In particular sulfur with valence 6 could wreak havoc of our estimates. I don’t know what happens if you allow an arbitrary number of S and P; I also don’t know if we would even want such all-sulfur molecules. The only number that I can report is again from the Kerber et al. paper: They also generated all molecular structures for nominal mass 150 Dalton and elements CHNOSiPSFClBrI, using the (unrealistic) fixed valences 3 for phosphorus and 2 for sulfur, resulting in 1 052 647 246 structures, compared to 615 977 591 molecular structures over elements CHNO. Yet, this small increase in structures (merely doubled, phew) should not lull us into a false sense of security: Not only the unrealistic valences, even more so the relatively small mass could mean that in truth, the number of structures with sulfur and phosphorus is substantially higher. I suggest we stick with the number 1080 and in the back of our minds, keep the note “it is likely even worse”.
It is not easy to grasp a number as large as 1080, so a few words to get a feeling:
- The number 1080 is 100 septemvigintillion, or 100 million billion billion billion billion billion billion billion billions. If we have a name for it, it cannot be that bad.
- The observable universe contains an estimated 1080 atoms. If we had the technology to build a computer that uses every single atom of the observable universe as its memory, and where we need only a single atom to store the complete structure of a small molecule, then the observable universe would be “just right” to store all small molecules up to 1000 Dalton.
- Using the same technology, molecules up to 1010 Dalton would be absolutely impossible to store, and 1100 Dalton would be absurd. For molecules up to 2000 Dalton you would need 1080 observable universes. Alternatively, a technology that puts a complete universe into a single atom, and does so for each and every atom of this universe. See the final scene of Men in Black.
- For comparison, the total amount of storage on planet Earth is, at the moment, something like 200 zettabytes, mostly on magnetic tapes. If we could store every molecular structure in 2 bytes, this would allow us to store 1023 molecular structures. If we could now again fold all the storage into a single byte, and again, and again, we reach – after four iterations of folding – the required memory.
- If we have a computer enumerating molecular structures at a rate of 1 billion structures per second, then we could enumerate 3.15 · 1016 structures per year, and it would take 3.17 · 1063 years to enumerate them all. For comparison, the estimated age of the universe is 1.38 · 1010 years. We would need more than 1050 universes to finish our calculations, where in each universe we have to start our computations with the big bang.
- Maybe, it helps if we use all computers that exist on planet Earth? Not really; there are maybe 10 billion computers (including smartphones) on Earth, but let’s make it 1000 billion, to be on the safe side. The required time to enumerate all structures drops to 3.17 · 1051 years.
- But maybe, we can use a quantum computer? Grover’s algorithm brings down the running times to
if we have to consider n objects. Again assuming that our quantum computer could do 1 billion such computations per second, we would end up with a running time of 1031 seconds, or 3.17 · 1023 years. That is still a looong time. There might be smarter ways of processing all structures on a quantum computer than using Grover’s algorithm; but so far, few such algorithms for even fewer problems have been found.
Now, 1080 is a large number, and you might thing, “this is the reason why dealing with small molecules is so complicated!” But that is a misconception. It is trivial to find much larger numbers that a computer scientist has to deal with every day; just a few examples from bioinformatics: The number of protein sequences of length 100 is 1.26 · 10130. Yet, we can easily work with longer protein sequences. The number of pairwise alignments for two sequences of length 1000 is 2.07 · 10600. Yet, every bioinformatics student learns during his/her first year how to find the optimal alignment between two sequences, sequences that may be much longer than 1000 bases. The thing is, sequences/strings are simple structures, and we have learned to look only for the interesting, i.e. optimal alignments. (Discrete optimization is great!) What makes dealing with small molecule structures complicated is that these structures are themselves rather complicated (graphs, when even trees can be a horror, ask someone from phylogenetics) plus at the same time, there are so many, which prevents us from simply enumerating them all, then doing the complicated stuff for every structure.
That’s all, folks! Hope it helps.
Yet another blog
Hi all, I thought I put my blog post (singular) into its own category. Not sure about the title, that may change. Why another blog when there is already this great blog on metabolomics and mass spectrometry? Because here I may talk about computational stuff as well, such as failed evaluations of machine learning methods (that one never gets old). I hope to write something once every four fortnights, let’s see how that works out. :shrug:
Times are changing but order matters
Our preprint Times are changing but order matters: Transferable prediction of small molecule liquid chromatography retention times is finally available on chemRxiv! Congratulations to Fleming and all authors.
In short, we show that prediction of retention times is a somewhat ill-posed problem, as retention times vary substantially even for nominally identical condition. Next, we show that retention order is much better preserved; but even retention order changes when the chromatographic conditions (column, mobile phase, temperature) vary. Third, we show that we can predict a retention order index (ROI) based on the compound structure and the chromatographic conditions. And finally, we show that one can easily map ROIs to retention times, even for target datasets that the machine learning model has never seen during training. Even for chromatographic conditions (column, pH) that are not present in the training data. Even for “novel compounds” that were not in the training data. Even if all of those restrictions hit us simultaneously.
In principle, this means that transferable retention time prediction (for novel compounds and novel chromatographic conditions) is “solved” for reversed-phase chromatography. There definitely is room for improvement, but that mainly requires more training data, not better methods. For that, we need your help: We need you, the experimentalists, to provide your reference LC-MS datasets. It does not matter what compounds are in there, it does not matter what chromatographic setup you used; as long as it is references data measured from standards (meaning that you know exactly each compound in the dataset), and as long as you tell us the minimum metadata, this will improve prediction quality.
You can post your data wherever you like, but you can also upload them to RepoRT so that in the future, scientists from machine learning can easily access them. We now provide a web app that makes uploading really simple. If you are truly interested in retention time prediction, then this should be well-invested 30 min.
False Discovery Rates for metabolite annotation: Why accurate estimation is impossible, and why this should not stop us from trying
I recently gave a talk at the conference of the Metabolomics society. After the talk, Oliver Fiehn asked, “when will we finally have FDR estimation in metabolite annotation?” This is a good question: False Discovery Rates (FDR) and FDR estimation have been tremendously helpful in genomics, transcriptomics and proteomics. In particular, FDRs have been extremely helpful for peptide annotation in shotgun proteomics. Hence, when will FDR estimation finally become a reality for metabolite annotation from tandem mass spectrometry (MS/MS) data? After all, the experimental setup of shotgun proteomics and untargeted metabolomics using Liquid Chromatography (LC) for separation, are highly similar. By the way, if I talk about metabolites below, this is meant to also include other small molecules of biological interest. From the computational method standpoint, they are indistinguishable.
My answer to this question was one word: “Never.” I was about to give a detailed explanation for this one-word answer, but before I could say a second word, the session chair said, “it is always good to close the session on a high note, so let us stop here!” and ended the session. (Well played, Tim Ebbels.) But this is not how I wanted to answer this question! In fact, I have been thinking about this question for several years now; as noted above, I believe that it is an excellent question. Hence, it might be time share my thoughts on the topic. Happy to hear yours! I will start off with the basics; if you are familiar with the concepts, you can jump to the last five paragraphs of this text.
The question that we want to answer is as follows: We are given a bag of metabolite annotations from an LC-MS/MS run. For every query spectrum, this is the best fit (best-scoring candidate) from the searched database, and will be called “hit” in the following. Can we estimate the fraction of hits that are incorrect? Can we do so for a subset of hits? More precisely, we will sort annotations by some score, such as the cosine similarity for spectral library search. If we only accept those hits with score above (or below, it does not matter) a certain threshold, can we estimate the ratio of incorrect hits for this particular subset? In practice, the user selects an arbitrary FDR threshold (say, one percent), and we then find the smallest score threshold so that the hits with score above the score threshold have an estimated FDR below or equal to the FDR threshold. (Yes, there are two thresholds, but we can handle that.)
Let us start with the basic definition. For a given set of annotations, the False Discovery Rate (FDR) is the number of incorrect annotations, divided by the total number of annotations. FDR is usually recorded as a percentage. To compute FDR, you have to have complete knowledge; you can only compute it if you know upfront which annotations are correct and which are incorrect. Sad but true. This value is often referred to as “exact FDR” or “true FDR”, to distinguish it from the estimates we want to determine below. Obviously, you can compute exact FDR for metabolite annotations, too; the downside is that you need complete knowledge. Hence, this insight is basically useless, unless your are some demigod or all-knowing demon. For us puny humans, we do not know upfront which annotations are correct and which are incorrect. The whole concept of FDR and FDR estimation would be useless if we knew: If we knew, we could simply discard the incorrect hits and continue to work with the correct ones.
To this end, a method for FDR estimation tries to estimate the FDR of a given set of annotations, without having complete knowledge. It is important to understand the part that says, “tries to estimate”. Just because a method claims it is estimating FDR, does not mean it is doing a good job, or even anything useful. For example, consider a random number generator that outputs random values between 0 and 1: This IS an FDR estimation method. It is neither accurate nor useful, but that is not required in the definition. Also, a method for FDR estimation may always output the same, fixed number (say, always-0 or always-1). Again, this is a method for FDR estimation; again, it is neither accurate nor useful. Hence, be careful with papers that claim to introduce an FDR estimation method, but fail to demonstrate that these estimates are accurate or at least useful.
But how can we demonstrate that a method for FDR estimation is accurate or useful? Doing so is somewhat involved because FDR estimates are statistical measures, and in theory, we can only ask if they are accurate for the expected value of the estimate. Yet, if someone presents a novel methods for FDR estimation, the minimum to ask for is a series of q-value plots that compare estimated q-values and exact q-values: A q-value is the smallest FDR for which a particular hit is part of the output. Also, you might want to see the distribution of p-values, which should be uniform. You probably know p-values; if you can estimate FDR, chances are high that you can also estimate p-values. Both evaluations should be done for multiple datasets, to deal with the stochastic nature of FDR estimation. Also, since you have to compute exact FDRs, the evaluation must be done for reference datasets where the true answer is known. Do not confuse “the true answer is known” and “the true answer is known to the method“; obviously, we do not tell our method for FDR estimation what the true answer is. If a paper introduces “a method for FDR estimation” but fails to present convincing evaluations that the estimated FDRs are accurate or at least useful, then you should be extremely careful.
Now, how does FDR estimation work in practice? In the following, I will concentrate on shotgun proteomics and peptide annotation, because this task is most similar to metabolomics. There, target-decoy methods have been tremendously successful: You transform the original database you search in (called target database in the following) into a second database that contains only candidates that are incorrect. This is the decoy database The trick is to make the candidates from the decoy database “indistinguishable” from those in the target database, as further described below. In shotgun proteomics, it is surprisingly easy to generate a useful decoy database: For every peptide in the target database, you generate a peptide in the decoy database for which you read the amino acid sequence from back to front. (In more detail, you leave the last amino acid of the peptide untouched, for reasons that are beyond what I want to discuss here.)
To serve its purpose, a decoy database must fulfill three conditions: (i) There must be no overlap between target and decoy database; (ii) all candidates from the decoy database must never be the correct answer; and (iii), false hits in the target database have the same probability to show up as (always false) hits from the decoy database. For (i) and (ii), we can be relatively relaxed: We can interpret “no overlap” as “no substantial overlap”. This will introduce a tiny error in our FDR estimation, which is presumably irrelevant in comparison to the error that is an inevitable part of FDR estimation. For (ii), this means that whenever a search with a query spectrum returns a candidate from the target database, this is definitely not the correct answer. The most important condition is (iii), and if we look more precisely, we will even notice that we have to demand more: That is, the score distribution of false hits from the target database is identical to the score distribution of hits from the decoy database. If our decoy database fulfills all three conditions, then we can use a method such as Target-Decoy Competition and utilize hits from the decoy database to estimate the ration of incorrect hits from the target database. Very elegant in its simplicity.
Enough of the details, let us talk about untargeted metabolomics! Can we generate a decoy database that fulfills the three requirements? Well — it is difficult, and you might think that this is why I argue that FDR estimation is impossible here: Looks like we need a method to produce metabolite structure that look like true metabolites (or, more generally, small molecules of biological interest — it does not matter). Wow, that is already hard — we cannot simply use random molecular structure, because they will not look like the real thing, see (iii). In fact, a lot of research is currently thrown at this problem, as it would potentially allow us to find the next super-drug. Also, how could we guarantee not to accidentally generate a true metabolite, see (ii)? Next, looks like we need a method to simulate a mass spectrum for a given (arbitrary) molecular structure. Oopsie daisies, that is also pretty hard! Again, ongoing research, far from being solved, loads of papers, even a NeurIPS competition coming up.
So, are these the problems we have to solve to do FDR estimation, and since we cannot do those, we also cannot do FDR? In other words, if — in a decade or so — we would finally have a method that can produce decoy molecular structures, and another method that simulates high-quality mass spectra, would we have FDR estimation? Unfortunately, the answer is, No. In fact, we do not even need those methods: In 2017, my lab developed a computational method that transforms a target spectral library into a decoy spectral library, completely avoiding the nasty pitfalls of generating decoy structures and simulating mass spectra. Also, other computational methods (say, naive Bayes) completely avoid generating a decoy database.
The true problem is that we are trying to solve a non-statistical problem with a statistical measure, and that is not going to work, no matter how much we think about the problem. I repeat the most important sentence from above: “False hits in the target database have the same probability to show up as hits from the decoy database.” This sentence, and all stochastic procedure for FDR estimation, assume that a false hit in the target database is something random. In shotgun proteomics, this is a reasonable assumption: The inverted peptides we used as decoys basically look random, and so do all false hits. The space of possible peptides is massive, and the target peptides lie almost perfectly separated in this ocean of non-occurring peptides. Biological peptides are sparse and well-separated, so to say. But this is not the case for metabolomics and other molecules of biological interest. If an organism has learned how to make a particular compound, it will often also be able to synthesize numerous compounds that are structurally extremely similar. A single hydrogen replaced by a hydroxy group, or vice versa. A hydroxy group “moving by a single carbon atom”. Everybody who has ever looked at small molecules, will have noticed that. Organisms invest a lot of energy to make proteins for exactly this purpose. But this is not only a single organism; the same happens in biological communities, such as the microbiota in our intestines or on our skin. It even happens when no organisms are around. In short: No metabolite is an island.
Sadly, this is the end of the story. Let us assume that we have identified small molecule A for a query MS/MS when in truth, the answer should be B. In untargeted metabolomics and related fields, this usually means that A and B are structurally highly similar, maybe to the point of a “moving hydroxy group”. Both A and B are valid metabolites. There is nothing random or stochastic about this incorrect annotation. Maybe, the correct answer B was not even in the database we searched in; potentially, because it is a “novel metabolite” currently not known to mankind. Alternatively, both compounds were in the database, and our scoring function for deciding on the best candidate simply did not return the correct answer. This will happen, inevitably: Otherwise, you again need a demigod or demon to build the scoring function. Consequently, speaking about the probability of an incorrect hit in the target database, cannot catch the non-random part of such incorrect hits. There is no way to come up with an FDR estimation method that is accurate, because the process itself is not stochastic. Maybe, some statisticians will develop a better solution some day, but I argue that there is no way to ever “solve it for good”, given our incomplete knowledge of what novel metabolites remain to be found out there.
Similar arguments, by the way, hold true for the field of shotgun metaproteomics: There, our database contains peptides from multiple organisms. Due to homologous peptide sequences in different organisms, incorrect hits are often not random. In particular, there is a good chance that if PEPTIDE is in your database, then so is PEPITDE. Worse, one can be in the database you search and one in your biological sample. I refrain from discussing further details; after all, we are talking about metabolites here.
But “hey!”, you might say, “Sebastian, you have published methods for FDR estimation yourself!” Well, that is true: Beyond the 2017 paper mentioned above, the confidence score of COSMIC is basically trying to estimate the Posterior Error Probability of a hit, which is a statistical measure again closely related to FDRs and FDR estimation. Well, you thought you got me there, did you? Yet, do you remember that above, I talked about FDR estimation methods that are accurate or useful? The thing is: FDR estimation methods from shotgun proteomics are enviably accurate, with precise estimates at FDR 1% and below. Yet, even if our FDR estimation methods in metabolomics can never be as accurate as those from shotgun proteomics, that does not mean they cannot be useful! We simply have to accept the fact that our numbers will not be as accurate, and that we have to interpret those numbers with a grain of salt.
The thing is, ballpark estimates can be helpful, too. Assume you have to jump, in complete darkness, into a natural pool of water below. I once did that, in a cave in New Zealand. It was called “cave rafting”, not sure if they still offer that type of organized madness. (Just checked, it does, highly recommended.) Back then, in almost complete darkness, our guide told me to jump; that I would fall for about a meter, and that the water below was two meters deep. I found this information to be extremely reassuring and helpful, but I doubt it was very accurate. I did not do exact measurements after the jump, but it is possible that I fell for only 85cm; possibly, the water was 3m deep. Yet, what I really, really wanted to know at that moment, was: Is it an 8m jump into a 30cm pond? I would say the guide did a good job. His estimates were useful.
I stress that my arguments should not be taken as an excuse to do a lazy evaluation. Au contraire! As a field, we must insist that all methods marketed as FDR estimation methods, are evaluated extensively as such. FDR estimations should be as precise as possible, and evaluations as described above are mandatory. Because only this can tell us how for we can trust the estimates. Because only this can convince us that estimates are indeed useful. Trying to come up with more accurate FDR estimates is a very, very challenging task, and trying to do so may be in vain. But remember: We choose to do these things, not because they are easy, but because they are hard.
I got the impression that few people in untargeted metabolomics and related fields are familiar with the concept of FDR and FDR estimation for annotation. This strikes me as strange, given the success of these concepts in other OMICS fields. If you want to learn more, I do not have the perfect link or video for you, but I tried my best to explain it in my videos about COSMIC, see here. If you have a better introduction, let me know!
Funny side note: If you were using a metascore, your FDR estimates from target-decoy competition would always be 0%. As noted, a method for FDR estimation must not return accurate or useful values, and a broken scoring can easily also break FDR estimation. Party on!
Prague workshop will be streamed
Good news for those who want to attend the Prague workshop but were not admitted: The Prague workshop on computational mass spectrometry will be streamed, see here. You should get the necessary software installed beforehand if you want to join in.
IMPRS call for PhD student
The International Max Planck Research School at the Max Planck Institute for Chemical Ecology in Jena is looking for PhD students. One of the projects (Project 7) is from our group on “rethinking molecular networks”. Application deadline is April 19, 2024.
Mass spectrometry (MS) is the analytical platforms of choice for high-throughput screening of small molecules and untargeted metabolomics. Molecular networks were introduced in 2012 by the group of Pieter Dorrestein, and have found widespread application in untargeted metabolomics, natural products research and related areas. Molecular networking is basically a method of visualizing your data, based on the observation that similar tandem mass spectra (MS/MS) often correspond to compounds that are structurally similar. Constructing a molecular network allows us to propagate annotations through the network, and to annotate compounds for which no reference MS/MS data are available. Since its introduction, the computational method has received a few “updates”, including Feature-Based Molecular Networks and Ion Identity Molecular Networks. Yet, the fundamental idea of using the modified cosine to compare tandem mass spectra, has basically remained unchanged at the core of the method.
In this project, we want to “rethink molecular networks”, replacing the modified cosine by other measures of similarity, including fragmentation tree similarity, the Tanimoto similarity of the predicted fingerprints, and False Discovery Rate estimates. See the project description for details.
We are searching for a qualified and motivated candidate from bioinformatics, machine learning, cheminformatics and/or computer science who want to work in this exciting, quickly evolving interdisciplinary field. Please contact Sebastian Böcker in case of questions. Payment is 0.65 positions TV-L E13.
IMPRS: https://www.ice.mpg.de/129170/imprs
MPI-CE: https://www.ice.mpg.de/
SIRIUS & CSI:FingerID: https://bio.informatik.uni-jena.de/software/sirius/
Literature: https://bio.informatik.uni-jena.de/publications/ and https://bio.informatik.uni-jena.de/textbook-algoms/
Jena is a beautiful city and wine is grown in the region:
https://www.youtube.com/watch?v=DQPafhqkabc
https://www.google.com/search?q=jena&tbm=isch
https://www.study-in.de/en/discover-germany/german-cities/jena_26976.php
Prague workshop on computational MS overbooked
Unfortunately, the Prague Workshop on Computational Mass Spectrometry (April 15-17, 2024) is heavily overbooked. The organizers will try to stream the workshop and the recorded sessions will be made available online, so check there regularly.
The workshop is organized by Tomáš Pluskal and Robin Schmid (IOCB Prague). Marcus Ludwig (Bright Giant) and Sebastian will give a tutorial on SIRIUS, CANOPUS etc.
Topics of the workshop are: MZmine, SIRIUS, matchms, MS2Query, LOTUS, GNPS, MassQL, MASST, and Cytoscape.
Meet Sebastian at the DGMS conference in Freising
Meet Sebastian at the conference of the Deutsche Gesellschaft für Massenspektrometrie (DGMS 2024) in Freising! The conference is March 10-13, and Sebastian will give a keynote talk on Tuesday, March 12.
BTW, another keynote will be given by our close collaboration partner Michael Witting, also on March 12.
RepoRT has appeared in Nature Methods
Our paper “RepoRT: a comprehensive repository for small molecule retention times” has just appeared in Nature Methods. This is joint work with Michael Witting (Helmholtz Zentrum München) as part of the DFG project “Transferable retention time prediction for Liquid Chromatography-Mass Spectrometry-based metabolomics“. Congrats to Fleming, Michael and all co-authors! In case you do not have access to the paper, you can find the preprint here and a read-only version here.
RepoRT is a repository for retention times, that can be used for any computational method development towards retention time prediction. RepoRT contains data from diverse reference compounds measured on different columns with different parameters and in different labs. At present, RepoRT contains 373 datasets, 8809 unique compounds, and 88,325 retention time entries measured on 49 different chromatographic columns using varying eluents, flow rates, and temperatures. Access RepoRT here.
If you have measured a dataset with retention times of reference compounds (that is, you know all the compounds identities) then please, contribute! You can either upload it to GitHub yourself, or you can contact us in case you need help. In the near future, a web interface will become available that will make uploading data easier. There are a lot of data in RepoRT already, but don’t let that fool you; to reach a transferable prediction of retention time and order (see below), this can only be the start.
If you want to use RepoRT for machine learning and retention time or order prediction: We have done our best to curate RepoRT: We have searched and appended missing data and metadata; we have standardized data formats; we provide metadata in a form that is accessible to machine learning; etc. For example, we provide real-valued parameters (Tanaka, HSM) to describe the different column models, in a way that allows machine learning to transfer between different columns. Yet, be careful, as not all data are available for all compounds or datasets. For example, it is not possible to provide Tanaka parameters for all columns; please see the preprint on how you can work your way around this issue. Similarly, not all compounds that should have an isomeric SMILES, do have an isomeric SMILES; see again the preprint. If you observe any issues, please let us know. See this interesting blog post and this paper as well as our own preprint on why providing “clean data” as well as “good coverage” are so important issues for small molecule machine learning.
Bioinformatische Methoden in der Genomforschung muss leider ausfallen
Nach aktuellem Kenntnisstand muss das Modul “Bioinformatische Methoden in der Genomforschung” im WS 23/24 leider ausfallen. Wir dürfen die Mitarbeiterstelle nicht besetzen, die wir dafür zwingend brauchen. Wir haben gekämpft und argumentiert und alles getan was wir konnten, aber am Ende war es leider vergeblich. Das Modul findet voraussichtlich das nächste Mal im WS 25/26 statt.
Warnung: Im Zuge der Sparmaßnamen an der FSU Jena kann es in Zukunft häufiger zu sollen kurzfristigen Ausfällen kommen.
Meet Sebastian at the Munich Metabolomics Meeting
Sebastian will give a tutorial on using SIRIUS and beyond at the Munich Metabolomics Meeting 2023.
HUMAN EU PhD position is still open
Unfortunately, we have not been able to fill the PhD position for the HUMAN EU project so far. In case you are interested, please contact us!
Update: The position has been filled.
Neues Video zum Studium Bioinformatik
Im Rahmen des MINT Festivals in Jena hat Sebastian ein neues Video zum Studium der Bioinformatik aufgenommen: “Kleine Moleküle. Was uns tötet, was uns heilt“. Es richtet sich vom Vorwissen her an Schüler aus der Oberstufe, aber vielleicht können auch Schüler aus den Jahrgangsstufen darunter etwas mitnehmen. Das Video ist erst mal nur über diese Webseite zu erreichen, wird aber in Kürze bei YouTube hochgeladen.
Am Ende noch zwei Fragen: Erstens, welche Zelltypen im menschlichen Körper enthalten nicht die (ganze) DNA? Da war ich aus Zeitgründen bewusst schlampert; keine Regel in der Biologie ohne Ausnahme. Und zweitens, NMR Instumente werden häufig nicht mit flüssigem Stickstoff gekühlt, sondern mit… was? Wie so oft geht es dabei ums liebe Geld.
Meet Nils, Wei, Fleming and Sebastian at GCB 2023
Meet us at the GCB 2023 in Hamburg! Nils, Wei and Fleming are going to present posters, and Sebastian will give a keynote talk.
Retention time repository preprint out now
The RepoRT (well, Repository for Retention Times, you guessed it) preprint is available now. It has been a massive undertaking to get to this point; honestly, we did not expect it to be this much work. It is about diverse reference compounds measured on different columns with different parameters and in different labs. At present, RepoRT contains 373 datasets, 8809 unique compounds, and 88,325 retention time entries measured on 49 different chromatographic columns using varying eluents, flow rates, and temperatures. Access RepoRT here.
If you have measured a dataset with retention times of reference compounds (that is, you know all the compounds identities) then please, contribute! You can either upload it to GitHub yourself, or you can contact us in case you need help. In the near future, a web interface will become available that will make uploading data easier. There are a lot of data in RepoRT already, but don’t let that fool you; to reach a transferable prediction of retention time and order (see below), this can only be the start.
If you want to do anything with the data, be our guests! It is available under the Creative Commons License CC-BY-SA.
If you want to use RepoRT for machine learning and retention time or order prediction, then, perfect! That is what we intended it for. 🙂 We have done our best to curate RepoRT: We have searched and appended missing data and metadata; we have standardized data formats; we provide metadata in a form that is accessible to machine learning; etc. For example, we provide real-valued parameters (Tanaka, HSM) to describe the different column models, in a way that allows machine learning to transfer between different columns. Yet, be careful, as not all data are available for all compounds or datasets. For example, it is not possible to provide Tanaka parameters for all columns; please see the preprint on how you can work your way around this issue. Similarly, not all compounds that should have an isomeric SMILES, do have an isomeric SMILES; see again the preprint. If you observe any issues, please let us know.